题目内容
 (2013•梧州一模)如图,将边长为4的正方形纸片ABCD折叠,使点B落在AD边上的M处(点M不与A、D重合),点C落在点N处,MN与CD交于点P,折痕为EF,则△PDM的周长是( )
(2013•梧州一模)如图,将边长为4的正方形纸片ABCD折叠,使点B落在AD边上的M处(点M不与A、D重合),点C落在点N处,MN与CD交于点P,折痕为EF,则△PDM的周长是( )分析:首先设AE=x,AM=y,则BE=EM=4-x,MD=4-y,在Rt△AEM中,由勾股定理得:AE2+AM2=EM2,可得16-y2=8x,易证得Rt△AEM∽Rt△DMP,然后由相似三角的性质,求得答案.
解答:解:设AE=x,AM=y,则BE=EM=4-x,MD=4-y,
在Rt△AEM中,由勾股定理得:AE2+AM2=EM2,
∴x2+y2=(4-x)2,
解得:16-y2=8x,
∵∠EMP=90°,
∴∠AEM+∠AME=90°,∠DMP+∠AME=90°,
∴∠AEM=∠DMP,
∵∠A=∠D,
∴Rt△AEM∽Rt△DMP,
∴
=
,
即
=
,
∴△PDM的周长是:8.
故选B.
在Rt△AEM中,由勾股定理得:AE2+AM2=EM2,
∴x2+y2=(4-x)2,
解得:16-y2=8x,
∵∠EMP=90°,
∴∠AEM+∠AME=90°,∠DMP+∠AME=90°,
∴∠AEM=∠DMP,
∵∠A=∠D,
∴Rt△AEM∽Rt△DMP,
∴
| AE+AM+EM |
| DM+DP+PM |
| AE |
| MD |
即
| x+y+4-x |
| DM+DP+PM |
| x |
| 4-y |
∴△PDM的周长是:8.
故选B.
点评:此题考查了折叠的性质、正方形的性质、相似三角形的判定与性质以及勾股定理.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
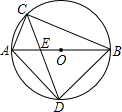 (2013•梧州一模)已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,交AB于E,则CD的长是
(2013•梧州一模)已知在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,交AB于E,则CD的长是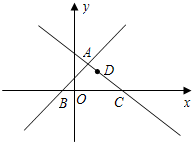 (2013•梧州一模)如图,在平面直角坐标系xOy中,直线y=x+1与y=-
(2013•梧州一模)如图,在平面直角坐标系xOy中,直线y=x+1与y=- (2013•梧州一模)如图,在3×3的正方形网格中,每个小正方形的边长为1,A、B两点在网格格点上,若C点也在网格格点上,以A、B、C三点为顶点的三角形的面积为1,则满足条件的点C的个数是( )
(2013•梧州一模)如图,在3×3的正方形网格中,每个小正方形的边长为1,A、B两点在网格格点上,若C点也在网格格点上,以A、B、C三点为顶点的三角形的面积为1,则满足条件的点C的个数是( )