题目内容
圆内接四边形ABCD,BC=CD,并且BD与AC相交于点E,BE:ED=3:4,则AD:AB=
- A.3:4
- B.4:3
- C.1:1
- D.9:16
C
分析:根据园内接四边形和圆周角定理,可证△AED∽△BEC,△AEB∽△DEC,再利用其对应边成比例得出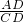 =
= 和
和 =
= ,然后相比即可得出答案.
,然后相比即可得出答案.
解答: 解:如图所示,
解:如图所示,
∵四边形ABCD是园内接四边形,
∴△AED∽△BEC,
∴ =
= =
= ,
,
∴△AEB∽△DEC,
∴ =
= =
= ,
,
又∵BC=CD,
∴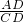 =
= ,
,
∴ =
= ,
,
∴ =
= .
.
故选C.
点评:此题主要考查学生对相似三角形的判定与性质和圆周角定理的理解与掌握,解答此题的关键是根据园内接四边形和圆周角定理,求证△AED∽△BEC,△AEB∽△DEC.
分析:根据园内接四边形和圆周角定理,可证△AED∽△BEC,△AEB∽△DEC,再利用其对应边成比例得出
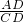 =
= 和
和 =
= ,然后相比即可得出答案.
,然后相比即可得出答案.解答:
 解:如图所示,
解:如图所示,∵四边形ABCD是园内接四边形,
∴△AED∽△BEC,
∴
 =
= =
= ,
,∴△AEB∽△DEC,
∴
 =
= =
= ,
,又∵BC=CD,
∴
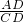 =
= ,
,∴
 =
= ,
,∴
 =
= .
.故选C.
点评:此题主要考查学生对相似三角形的判定与性质和圆周角定理的理解与掌握,解答此题的关键是根据园内接四边形和圆周角定理,求证△AED∽△BEC,△AEB∽△DEC.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,在圆内接四边形ABCD中,AB=AD,∠BAD=60°,AC=a,则四边形ABCD的面积为
如图,在圆内接四边形ABCD中,AB=AD,∠BAD=60°,AC=a,则四边形ABCD的面积为 如图,圆内接四边形ABCD的对角线AC平分∠BCD,BD交AC于点F,过点A作圆的切线AE交CB的延长线于E.求证:①AE∥BD; ②AD2=DF•AE.
如图,圆内接四边形ABCD的对角线AC平分∠BCD,BD交AC于点F,过点A作圆的切线AE交CB的延长线于E.求证:①AE∥BD; ②AD2=DF•AE. (1997•新疆)已知如图,∠EAD是圆内接四边形ABCD的一个外角,则( )
(1997•新疆)已知如图,∠EAD是圆内接四边形ABCD的一个外角,则( )