题目内容
 如图,正六边形ABCDEF的边长为4,两顶点A、B分别在x轴和y轴上运动,则顶点D到原点O的距离的最大值和最小值的乘积为
如图,正六边形ABCDEF的边长为4,两顶点A、B分别在x轴和y轴上运动,则顶点D到原点O的距离的最大值和最小值的乘积为
- A.

- B.48
- C.32
- D.
B
分析:根据已知得出D点的两个特殊位置,进而求出即可.
解答: 解:当O、D、AB中点共线时,OD有最大值和最小值,
解:当O、D、AB中点共线时,OD有最大值和最小值,
如图,BD=4 ,BK=2,
,BK=2,
∴DK= =
= ,OK=BK=2,
,OK=BK=2,
∴OD的最大值为:2+ ,
,
同理,最小值为: -2,
-2,
∴顶点D到原点O的距离的最大值和最小值的乘积为:(2+ )(
)( -2)=48.
-2)=48.
故选:B.
点评:此题主要考查了正多边形的性质以及坐标轴的几何变换,做此类问题时,要先由特殊点考虑进行计算.
分析:根据已知得出D点的两个特殊位置,进而求出即可.
解答:
 解:当O、D、AB中点共线时,OD有最大值和最小值,
解:当O、D、AB中点共线时,OD有最大值和最小值,如图,BD=4
 ,BK=2,
,BK=2,∴DK=
 =
= ,OK=BK=2,
,OK=BK=2,∴OD的最大值为:2+
 ,
,同理,最小值为:
 -2,
-2,∴顶点D到原点O的距离的最大值和最小值的乘积为:(2+
 )(
)( -2)=48.
-2)=48.故选:B.
点评:此题主要考查了正多边形的性质以及坐标轴的几何变换,做此类问题时,要先由特殊点考虑进行计算.

练习册系列答案
相关题目
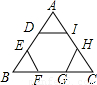
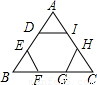
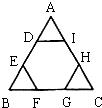 18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是
18、如图,正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上,则这个正六边形的边长是