题目内容
 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD= BC,CE=
BC,CE= AC,BE、AD相交于点F,连接DE,则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DF•DA;④AF•BE=AE•AC,正确的结论有
AC,BE、AD相交于点F,连接DE,则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DF•DA;④AF•BE=AE•AC,正确的结论有
- A.4个
- B.3个
- C.2个
- D.1个
A
分析:本题是开放题,对结论进行一一论证,从而得到答案.
①利用△ABD≌△BCE,再用三角形的一个外角等于与它不相邻的两个内角和,即可证∠AFE=60°;
②从CD上截取CM=CE,连接EM,证△CEM是等边三角形,可证明DE⊥AC;
③△BDF∽△ADB,由相似比则可得到CE2=DF•DA;
④只要证明了△AFE∽△BAE,即可推断出AF•BE=AE•AC.
解答: 解:∵△ABC是等边三角形
解:∵△ABC是等边三角形
∴AB=BC=AC,∠BAC=∠ABC=∠BCA=60°
∵BD= BC,CE=
BC,CE= AC
AC
∴BD=EC
∴△ABD≌△BCE
∴∠BAD=∠CBE,
∵∠ABE+∠EBD=60°
∴∠ABE+∠CBE=60°
∵∠AFE是△ABF的外角
∴∠AFE=60°
∴①是对的;
如图,从CD上截取CM=CE,连接EM,则△CEM是等边三角形
∴EM=CM=EC
∵EC= CD
CD
∴EM=CM=DM
∴∠CED=90°
∴DE⊥AC,
∴②是对的;
由前面的推断知△BDF∽△ADB
∴BD:AD=DF:DB
∴BD2=DF•DA
∴CE2=DF•DA
∴③是对的;
在△AFE和△BAE中,∠BAE=∠AFE=60°,∠AEB是公共角
∴△AFE∽△BAE
∴AF•BE=AE•AC
∴④是正确的.
故选A.
点评:本题主要应用到了三角形外角与内角的关系,直角三角形的判定,全等三角形和相似三角形的判定及性质,内容较多,较为复杂.
分析:本题是开放题,对结论进行一一论证,从而得到答案.
①利用△ABD≌△BCE,再用三角形的一个外角等于与它不相邻的两个内角和,即可证∠AFE=60°;
②从CD上截取CM=CE,连接EM,证△CEM是等边三角形,可证明DE⊥AC;
③△BDF∽△ADB,由相似比则可得到CE2=DF•DA;
④只要证明了△AFE∽△BAE,即可推断出AF•BE=AE•AC.
解答:
 解:∵△ABC是等边三角形
解:∵△ABC是等边三角形∴AB=BC=AC,∠BAC=∠ABC=∠BCA=60°
∵BD=
 BC,CE=
BC,CE= AC
AC∴BD=EC
∴△ABD≌△BCE
∴∠BAD=∠CBE,
∵∠ABE+∠EBD=60°
∴∠ABE+∠CBE=60°
∵∠AFE是△ABF的外角
∴∠AFE=60°
∴①是对的;
如图,从CD上截取CM=CE,连接EM,则△CEM是等边三角形
∴EM=CM=EC
∵EC=
 CD
CD∴EM=CM=DM
∴∠CED=90°
∴DE⊥AC,
∴②是对的;
由前面的推断知△BDF∽△ADB
∴BD:AD=DF:DB
∴BD2=DF•DA
∴CE2=DF•DA
∴③是对的;
在△AFE和△BAE中,∠BAE=∠AFE=60°,∠AEB是公共角
∴△AFE∽△BAE
∴AF•BE=AE•AC
∴④是正确的.
故选A.
点评:本题主要应用到了三角形外角与内角的关系,直角三角形的判定,全等三角形和相似三角形的判定及性质,内容较多,较为复杂.

练习册系列答案
相关题目
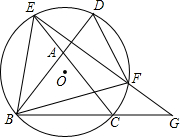 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.