题目内容
【题目】如图,平行四边形ABCD的对角线AC,BD交于点O,△AOD是正三角形,AD=4,则平行四边形ABCD的面积为 . 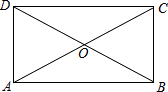
【答案】16 ![]()
【解析】解:作DE⊥AC于E, ∴∠AED=90°.
∵△AOD是正三角形,
∴AD=DO=AO,AO=EO= ![]() AO,∠ADO=∠DAO=60°,
AO,∠ADO=∠DAO=60°,
∴∠ADE=30°.
∵AD=4,
∴AE=2.
在Rt△ADE中,由勾股定理,得
DE=2 ![]() ,
,
∴S△AOD= ![]() ×4×2
×4×2 ![]() =4
=4 ![]() .
.
∵四边形ABCD是平行四边,
∴S△AOD=S△DOC=S△BOC=S△AOB ,
∴平行四边形ABCD的面积=4×4 ![]() =16
=16 ![]() .
.
所以答案是:16 ![]() .
.
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.

练习册系列答案
相关题目