题目内容
【题目】已知
的半径为
，弦
，
，
，则
、
之间的距离为________．
【答案】
或
．
【解析】
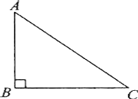
首先作AB、CD的垂线EF，然后根据垂径定理求得CE=DE=10cm，AF=BF=24cm；再在直角三角形OED和直角三角形OBF中，利用勾股定理求得OE、OF的长度；最后根据图示的两种情况计算EF的长度即可．
有两种情况.如图.过O作AB、CD的垂线EF，交AB于点F，交CD于点E.
∴EF就是AB、CD间的距离。
∵AB=48cm，CD=20cm，根据垂径定理，得CE=DE=10cm，AF=BF=24cm，
∵OD=OB=26cm，
∴在直角三角形OED和直角三角形OBF中，
∴OE=24cm，OF=10cm(勾股定理)，
∴①EF=24+10=34cm②EF=2410=14cm，
故答案为：34或14cm.
练习册系列答案
阅读快车系列答案
相关题目
【题目】抛物线
上部分点的横坐标
，纵坐标
的对应值如下表：
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
小聪观察上表，得出下面结论：①抛物线与轴的一个交点为
；②函数的最大值为
；③抛物线的对称轴是
；④在对称轴左侧，随增大而增大．其中正确有（ ）
A. 0个 B. 1个 C. 2个 D. 3个
