题目内容
如图①,直线AB的解析式为![]() (
(![]() )与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.
)与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.
⑴求C点的坐标;
⑵如图②,过![]() 作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
 | |||||
 | |||||
 | |||||
![]() ⑶在⑵的条
⑶在⑵的条![]() 件下,连接
件下,连接![]() 与⊙
与⊙![]() 交于点G,点P为劣弧GF上一个动点,连接GP与EF的延
交于点G,点P为劣弧GF上一个动点,连接GP与EF的延
![]() 长线交于H点,连接EP与OG交于I点,当P在劣弧GF运动时(不与G、F两点重合),
长线交于H点,连接EP与OG交于I点,当P在劣弧GF运动时(不与G、F两点重合),![]() 的值
的值![]() 是否发生变化,若不变,求其值,若发生变化,求出其值的变化范围.
是否发生变化,若不变,求其值,若发生变化,求出其值的变化范围.
解:(1)连结AC
∵![]() ∴B(2,0)
∴B(2,0)
∵∠ABO=60° ∴∠OAB=30°
∴AB=4,OA=![]()
∵AB是切线 ∴∠CAB=9![]() 0°,∠ACB=30°
0°,∠ACB=30°
∴AC=![]() ,CO=6
,CO=6
∴C(-6,0) --------3分

∴△![]() 为等边三角形 ∴
为等边三角形 ∴![]()
∵∠HGF=∠HEP ∠HFG=∠![]() =120°
=120°
∴△HGF≌△![]()
∴![]()
∴![]() =
=![]() =
=![]()

练习册系列答案
相关题目
 22、完成下列证明:
22、完成下列证明:

 23、如图,已知AB∥DE,∠BAE=∠EDC,AD⊥AE,垂足为A,请在下划线内补全求∠ADC的度数的解题过程或依据.
23、如图,已知AB∥DE,∠BAE=∠EDC,AD⊥AE,垂足为A,请在下划线内补全求∠ADC的度数的解题过程或依据.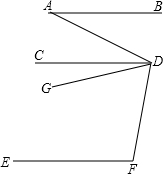
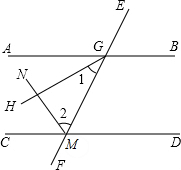 说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.
说理填空:如图,已知AB∥CD,GH平分∠AGM,MN平分∠CMG,请说明GH⊥MN的理由.