题目内容
(2009•大兴区二模)已知,抛物线y=ax2+bx+c过点A(-3,0),B(1,0),C(0, ),此抛物线的顶点为D.
),此抛物线的顶点为D.(1)求此抛物线的解析式;
(2)把△ABC的绕AB的中点M旋转180°,得到四边形AEBC.
①求E点的坐标;
②试判断四边形AEBC的形状,并说明理由.
(3)试探求:在直线BC上是否存在一点P,使得△PAD的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.

【答案】分析:(1)利用待定系数法就可以求出抛物线的解析式.
(2)①△ABC绕AB的中点M旋转180度.可知点E和点C关于点M对称.则E的坐标就可以求出.
②根据四边形AEBC的对角线互相平分,可知是平行四边形.Rt△ACO中,OC= ,OA=3得到∠ABE=30°,
,OA=3得到∠ABE=30°,
在Rt△COB中OC= ,OB=1得到∠CBO=60°,则∠CBE=∠CBO+∠ABE=60°+30°=90°因而ABEC是矩形.
,OB=1得到∠CBO=60°,则∠CBE=∠CBO+∠ABE=60°+30°=90°因而ABEC是矩形.
(3)点A与点A1也关于直线BC对称.连接A1D,与直线BC相交于点P,连接PA,则△PAD的周长最小.求出BC的解析式,A1D的解析式,两直线的交点就是所求的点.
解答:解:(1)∵y=ax2+bx+c过C(0, ),
),
∴
又y=ax2+bx+c过点A(-3,0)B(1,0),
∴
∴ ,
,
∴此抛物线的解析式为 .
.
(2)①△ABC绕AB的中点M旋转180度.可知点E和点C关于点M对称,
∴M(-1,0),C(0, ),
),
∴E(-2,- ).
).
②四边形AEBC是矩形.
∵△ABC绕AB的中点M旋转180°得到四边形AEBC,
∴△ABC≌△AEB
∴AC=EB,AE=BC,
∴AEBC是平行四边形在Rt△ACO中,OC= ,OA=3,
,OA=3,
∴∠CAB=30°
∵AEBC是平行四边形
∴AC∥BE,
∴∠ABE=30°在Rt△COB中
∵OC= ,OB=1,
,OB=1,
∴∠CBO=60°,
∴∠CBE=∠CBO+∠ABE=60°+30°=90°ABEC是矩形.
(3)假设在直线BC上存在一点P,使△PAD的周长最小.
因为AD为定值,所以使△PAD的周长最小,就是PA+PD最小;
∵AEBC是矩形,
∴∠ACB=90°,
∴A(-3,0)关于点C(0, )的对称点A1(3,2
)的对称点A1(3,2 ).
).
点A与点A1也关于直线BC对称.
连接A1D,与直线BC相交于点P,连接PA,则△PAD的周长最小.
∵B(1,0)、C(0, )
)
∴BC的解析式为
∵A1(3,2 )、D(-1,
)、D(-1, )
)
∴A1D的解析式为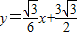 .
.
∴ ,
,
∴ ,
,
∴P的坐标为( ).
).
点评:本题主要靠了待定系数法求直线的解析式,以及函数图象交点坐标的求法.
(2)①△ABC绕AB的中点M旋转180度.可知点E和点C关于点M对称.则E的坐标就可以求出.
②根据四边形AEBC的对角线互相平分,可知是平行四边形.Rt△ACO中,OC=
 ,OA=3得到∠ABE=30°,
,OA=3得到∠ABE=30°,在Rt△COB中OC=
 ,OB=1得到∠CBO=60°,则∠CBE=∠CBO+∠ABE=60°+30°=90°因而ABEC是矩形.
,OB=1得到∠CBO=60°,则∠CBE=∠CBO+∠ABE=60°+30°=90°因而ABEC是矩形.(3)点A与点A1也关于直线BC对称.连接A1D,与直线BC相交于点P,连接PA,则△PAD的周长最小.求出BC的解析式,A1D的解析式,两直线的交点就是所求的点.
解答:解:(1)∵y=ax2+bx+c过C(0,
 ),
),∴

又y=ax2+bx+c过点A(-3,0)B(1,0),
∴

∴
 ,
,∴此抛物线的解析式为
 .
.(2)①△ABC绕AB的中点M旋转180度.可知点E和点C关于点M对称,
∴M(-1,0),C(0,
 ),
),∴E(-2,-
 ).
).②四边形AEBC是矩形.
∵△ABC绕AB的中点M旋转180°得到四边形AEBC,

∴△ABC≌△AEB
∴AC=EB,AE=BC,
∴AEBC是平行四边形在Rt△ACO中,OC=
 ,OA=3,
,OA=3,∴∠CAB=30°
∵AEBC是平行四边形
∴AC∥BE,
∴∠ABE=30°在Rt△COB中
∵OC=
 ,OB=1,
,OB=1,∴∠CBO=60°,
∴∠CBE=∠CBO+∠ABE=60°+30°=90°ABEC是矩形.
(3)假设在直线BC上存在一点P,使△PAD的周长最小.
因为AD为定值,所以使△PAD的周长最小,就是PA+PD最小;
∵AEBC是矩形,

∴∠ACB=90°,
∴A(-3,0)关于点C(0,
 )的对称点A1(3,2
)的对称点A1(3,2 ).
).点A与点A1也关于直线BC对称.
连接A1D,与直线BC相交于点P,连接PA,则△PAD的周长最小.
∵B(1,0)、C(0,
 )
)∴BC的解析式为

∵A1(3,2
 )、D(-1,
)、D(-1, )
)∴A1D的解析式为
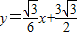 .
.∴
 ,
,∴
 ,
,∴P的坐标为(
 ).
).点评:本题主要靠了待定系数法求直线的解析式,以及函数图象交点坐标的求法.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目

 ,则电线杆AB的长为多少米?
,则电线杆AB的长为多少米?