题目内容
 (2013•下城区二模)已知在平面直角坐标系中,点A,B的坐标分别为A(2,-5),B(5,1).在同一个坐标系内画出满足下列条件的点(保留画图痕迹),并求出该点的坐标.
(2013•下城区二模)已知在平面直角坐标系中,点A,B的坐标分别为A(2,-5),B(5,1).在同一个坐标系内画出满足下列条件的点(保留画图痕迹),并求出该点的坐标.(1)在y轴上找一点C,使得AC+BC的值最小;
(2)在x轴上找一点D,使得AD-BD的值最大.
分析:(1)根据“两点之间,线段最短”可以推知,当点A、C、B三点共线时,AC+BC的值最小.所以作B关于y轴的对称点B′,连结AB′交y轴于点C.利用待定系数法求得A′B直线解析式,则根据解析式即可求得点C的坐标;
(2)根据“三角形两边之差小于第三条边”来找点D:作点B关于x轴的对称点B1,连结AB1延长交x轴于D.当A,B1,D三点共线时,AD-B1D=AB1,此时AD-B1D有最大值,最大值为AB1的长度.此时,点D在直线AB1上.
(2)根据“三角形两边之差小于第三条边”来找点D:作点B关于x轴的对称点B1,连结AB1延长交x轴于D.当A,B1,D三点共线时,AD-B1D=AB1,此时AD-B1D有最大值,最大值为AB1的长度.此时,点D在直线AB1上.
解答: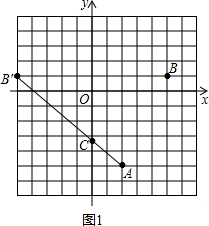 解:(1)C点如图1所示(或作B关于y轴的对称点B′,连结AB′交y轴于点C).
解:(1)C点如图1所示(或作B关于y轴的对称点B′,连结AB′交y轴于点C).
设直线AB′的解析式为y=kx+b(k≠0).
∵B(5,1),
∴B′(5,-1).
又∵A(2,-5),
∴
,
解得,
,
∴AB′直线解析式:y=-
x-
,
∴点C的坐标为(0,-
);
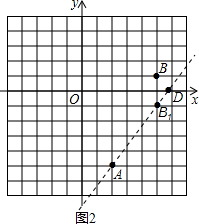
(2)D点如图所示,(作点B关于x轴的对称点B1,连结AB1延长交x轴于点D).
(理由:若A,B1,D三点不共线,根据三角形两边之差小于第三条边可得:AD-B1D<AB1,所以当A,B1,D三点共线时,AD-B1D=AB1,此时AD-B1D有最大值,最大值为AB1的长度.此时,点D在直线AB1上)
根据题意由A(2,-5),B1(5,-1)代入可得直线AB1的解析式为:y=
x-
,
∴当AD-BD有最大值时,点D的坐标为(
,0).
 解:(1)C点如图1所示(或作B关于y轴的对称点B′,连结AB′交y轴于点C).
解:(1)C点如图1所示(或作B关于y轴的对称点B′,连结AB′交y轴于点C).设直线AB′的解析式为y=kx+b(k≠0).
∵B(5,1),
∴B′(5,-1).
又∵A(2,-5),
∴
|
解得,
|
∴AB′直线解析式:y=-
| 6 |
| 7 |
| 23 |
| 7 |

∴点C的坐标为(0,-
| 23 |
| 7 |
(2)D点如图所示,(作点B关于x轴的对称点B1,连结AB1延长交x轴于点D).
(理由:若A,B1,D三点不共线,根据三角形两边之差小于第三条边可得:AD-B1D<AB1,所以当A,B1,D三点共线时,AD-B1D=AB1,此时AD-B1D有最大值,最大值为AB1的长度.此时,点D在直线AB1上)
根据题意由A(2,-5),B1(5,-1)代入可得直线AB1的解析式为:y=
| 4 |
| 3 |
| 23 |
| 3 |
∴当AD-BD有最大值时,点D的坐标为(
| 23 |
| 4 |
点评:本题综合考查了待定系数法求一次函数解析式,一次函数图象上点的坐标特征,两点之间线段最短以及三角形的三边关系等知识点.解题时,注意作图所依据的公理以及相关图形的性质.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目