题目内容
已知:⊙O分别与△ABC的两边AB、AC所在直线相切于点D、F,且OB=OC.
(1)如图1,若圆心O在边BC上,求证:AB=AC;
(2)如图2,若圆心O在△ABC的内部,求证:AB=AC;
(3)当小明完成以上两小题后,得出一个结论:若圆心O在△ABC的外部,AB=AC仍然成立.你同意他的说法吗?若同意,请证明;若不同意,请画图说明(不要求尺规作图).

(1)如图1,若圆心O在边BC上,求证:AB=AC;
(2)如图2,若圆心O在△ABC的内部,求证:AB=AC;
(3)当小明完成以上两小题后,得出一个结论:若圆心O在△ABC的外部,AB=AC仍然成立.你同意他的说法吗?若同意,请证明;若不同意,请画图说明(不要求尺规作图).

分析:(1)可由HL证得Rt△OBD≌Rt△OCF,从而得到∠B=∠C?AB=BC;
(2)连接OD,OF,BO,CO,也可由HL证得Rt△OBD≌Rt△OCF,得到∠DBO=∠FCO,由等边对等角得到∠OBC=∠OCB,故有∠ABC=∠ACB?AB=AC;
(3)通过作图,可知AB=AC不一定成立.
(2)连接OD,OF,BO,CO,也可由HL证得Rt△OBD≌Rt△OCF,得到∠DBO=∠FCO,由等边对等角得到∠OBC=∠OCB,故有∠ABC=∠ACB?AB=AC;
(3)通过作图,可知AB=AC不一定成立.
解答:(1)证明:连接OD,OF(如图1),
∵⊙O分别与△ABC的两边AB、AC所在直线相切于点D、F,
∴OD⊥AB,OF⊥AC,
∴∠BDO=∠CFO=90°.
∵在Rt△OBD和Rt△OCF中,
,
∴Rt△OBD≌Rt△OCF(HL).
∴∠B=∠C.
∴AB=AC.
(2)连接OD,OF,BO,CO(如图2),
∵⊙O分别与△ABC的两边AB、AC所在直线相切于点D、F,
∴OD⊥AB,OF⊥AC,
∴∠BDO=∠CFO=90°.
∵在Rt△OBD和Rt△OCF中,
,
∴Rt△OBD≌Rt△OCF(HL).
∴∠DBO=∠FCO.
∵OB=OC,
∴∠OBC=∠OCB.
∴∠DBO+∠OBC=∠FCO+∠OCB.
即∠ABC=∠ACB.
∴AB=AC.
(3)解:不一定成立,如右图.
∵⊙O分别与△ABC的两边AB、AC所在直线相切于点D、F,
∴OD⊥AB,OF⊥AC,

∴∠BDO=∠CFO=90°.
∵在Rt△OBD和Rt△OCF中,
|
∴Rt△OBD≌Rt△OCF(HL).
∴∠B=∠C.
∴AB=AC.
(2)连接OD,OF,BO,CO(如图2),
∵⊙O分别与△ABC的两边AB、AC所在直线相切于点D、F,
∴OD⊥AB,OF⊥AC,
∴∠BDO=∠CFO=90°.
∵在Rt△OBD和Rt△OCF中,
|
∴Rt△OBD≌Rt△OCF(HL).

∴∠DBO=∠FCO.
∵OB=OC,
∴∠OBC=∠OCB.
∴∠DBO+∠OBC=∠FCO+∠OCB.
即∠ABC=∠ACB.
∴AB=AC.
(3)解:不一定成立,如右图.
点评:本题考查了切线的性质、等腰三角形的判定和性质,全等三角形的判定和性质.利用全等三角形的性质求线段相等时证明线段相等的最常用方法之一,要熟练掌握.

练习册系列答案
相关题目
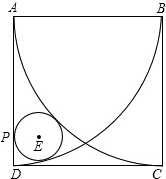 如图,正方形ABCD的边长为4,分别以A,B为圆心,4为半径画弧,已知圆E分别与两条弧相切,与AD相切于F,求圆E的半径.
如图,正方形ABCD的边长为4,分别以A,B为圆心,4为半径画弧,已知圆E分别与两条弧相切,与AD相切于F,求圆E的半径. (2013•资阳)如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线y=
(2013•资阳)如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线y= 分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.
分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.

 ∽
∽ ;
;  ,请求出点M的坐标,并写出以
,请求出点M的坐标,并写出以 为顶点,且过点M的抛物线的解析式;
为顶点,且过点M的抛物线的解析式;