ЬтФПФкШн
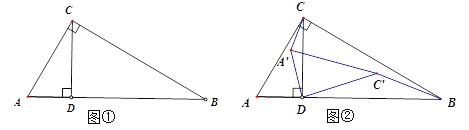
ЁОЬтФПЁПШчЭМЂйЃЌдкRtЁїABCжаЃЌЁЯC=90Ёу, ЁЯB=30Ёу,AC=1,CDЁЭABЃЌДЙзуЮЊDЃЌЯжНЋЁїACDШЦDЕуЫГЪБеыа§зЊ![]() ЕУЕНЁїAЁЎCЁЏD, а§зЊЪБМфЮЊtУыЃЌЁїACDШЦDЕуа§зЊЕФНЧЫйЖШ
ЕУЕНЁїAЁЎCЁЏD, а§зЊЪБМфЮЊtУыЃЌЁїACDШЦDЕуа§зЊЕФНЧЫйЖШ![]() /Уы(УПУызЊ10ЖШ) ЃЎ
/Уы(УПУызЊ10ЖШ) ЃЎ
ЃЈ1ЃЉа§зЊЪБМфt= УыЪБЃЌAЁЎCЁЏЁЮAB;
ЃЈ2ЃЉЁїACDШЦDЕуЫГЪБеыа§зЊвЛжмЃЈ3600ЃЉЃЌаББпACЩЈЙ§ЕФУцЛ§ЮЊ ЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌСЌНгAЁЏCЁЂ CЁЏBЃЎ
ЂйШє6ЃМtЃМ9ЃЌЧѓжЄЃК ![]() ЮЊЖЈжЕЃЛ
ЮЊЖЈжЕЃЛ
ЂкЕБtЃО9ЪБЃЌЩЯЪіНсТлЛЙГЩСЂТ№ЃПШчГЩСЂжБНгаДГіБШжЕЃЌВЛГЩСЂЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ6ЃЈ2ЃЉ![]() ЃЈ3ЃЉЂйжЄУїМћНтЮіЃЛЂкНсТлГЩСЂЃЌБШжЕШдЮЊ
ЃЈ3ЃЉЂйжЄУїМћНтЮіЃЛЂкНсТлГЩСЂЃЌБШжЕШдЮЊ![]() .
.
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉгЩа§зЊЕФа§зЊПЩЕУШєвЊ![]() ЁЮAB,ПЩ
ЁЮAB,ПЩ![]() ,МДПЩЧѓНтЃЛЃЈ2ЃЉгЩЬтвтПЩжЊаББпACЩЈЙ§ЕФУцЛ§ЮЊвдЕуDЮЊдВаФCDЃЌACБпЩЯЕФИпЮЊАыОЖЕФЛЗаЮЃЌРћгУДѓдВУцЛ§МѕШЅаЁдВУцЛ§МДПЩЧѓНтЃЛЃЈ3ЃЉЂйЕБ6ЃМtЃМ9ЪБЃЌжЊ60ЁуЃМІСЃМ90ЁуЃЌгЩЁї
,МДПЩЧѓНтЃЛЃЈ2ЃЉгЩЬтвтПЩжЊаББпACЩЈЙ§ЕФУцЛ§ЮЊвдЕуDЮЊдВаФCDЃЌACБпЩЯЕФИпЮЊАыОЖЕФЛЗаЮЃЌРћгУДѓдВУцЛ§МѕШЅаЁдВУцЛ§МДПЩЧѓНтЃЛЃЈ3ЃЉЂйЕБ6ЃМtЃМ9ЪБЃЌжЊ60ЁуЃМІСЃМ90ЁуЃЌгЩЁї![]() ЁзЁї
ЁзЁї![]() КЭЁї
КЭЁї![]() ЁзЁї
ЁзЁї![]() ЕУЕН
ЕУЕН![]() ЮЊЖЈжЕ
ЮЊЖЈжЕ![]() ЃЛЂкгУгыЂйЯрЭЌЕФЗНЗЈМДПЩЕУГіНсЙћ.
ЃЛЂкгУгыЂйЯрЭЌЕФЗНЗЈМДПЩЕУГіНсЙћ.
БОЬтНтЮіЃК
ЃЈ1ЃЉгЩ![]() ЁЮAB,ЕУ
ЁЮAB,ЕУ![]() ЃЌЁрt=6.
ЃЌЁрt=6.
ЃЈ2ЃЉЩшACБпЩЯЕФИпЮЊh,гЩ![]() .
.
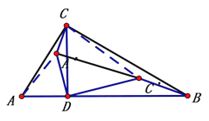
ЃЈ3ЃЉЂйЕБ6ЃМtЃМ9ЪБЃЌжЊ600ЃМ![]() ЃМ900
ЃМ900
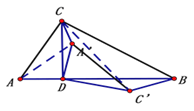
ШчЭМСЌНгAAЁЎЁЂC CЁЏ
гЩа§зЊЖЈвхжЊ
ЁЯAD AЁЎ=ЁЯCD CЁЏ=ЁЯ![]()
ЁпAD=AЁЎDЁЂCD= CЁЎD
ЁрЁїADAЁЎ ЁзЁїC D CЁЎЃЎ
ЁрЁЯAЁЎA D =ЁЯCЁЎCD ; ![]() ,
,
гжЁпЁЯCAD =ЁЯBCD =60O
ЁрЁїACAЁЎ ЁзЁїC BCЁЏ
Ёр![]() ЮЊЖЈжЕ.
ЮЊЖЈжЕ.
ЂкНсТлГЩСЂЃЌБШжЕШдЮЊ![]() .
.

 УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИ
УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИЁОЬтФПЁПШчЭМЫљЪОЃЌШєНЋРрЫЦгкaЁЂbЁЂcЁЂdЫФИіЭМЕФЭМаЮГЦзіЦНУцЭМЃЌдђЦфЖЅЕуЪ§ЁЂБпЪ§гыЧјгђЪ§жЎМфДцдкФГжжЙиЯЕЃЎЙлВьЭМbКЭБэжаЖдгІЕФЪ§жЕЃЌЬНОПМЦЪ§ЕФЗНЗЈВЂзїД№ЃЎ

ЃЈ1ЃЉЪ§вЛЪ§УПИіЭМжаИїгаЖрЩйИіЖЅЕуЁЂЖрЩйЬѕБпЃЌетаЉБпЮЇГіЖрЩйИіЧјгђВЂЬюБэЃК
ЦНУцЭМ | a | b | c | d |
ЖЅЕуЪ§(S) | 7 | |||
БпЪ§(M) | 9 | |||
ЧјгђЪ§(N) | 3 |
ЃЈ2ЃЉИљОнБэжаЪ§жЕЃЌаДГіЦНУцЭМЕФЖЅЕуЪ§ЁЂБпЪ§ЁЂЧјгђЪ§жЎМфЕФвЛжжЙиЯЕЮЊ ЃЛ
ЃЈ3ЃЉШчЙћвЛИіЦНУцЭМга20ИіЖЅЕуКЭ11ИіЧјгђЃЌФЧУДРћгУЃЈ2ЃЉжаЕУГіЕФЙиЯЕПЩжЊетИіЦНУцЭМга ЬѕБпЃЎ

