题目内容
如图，一辆吊车的吊臂以60°倾角倾斜于水平面，如果这辆吊车支点A距离地面的高AB为2m，且点A到铅垂线ED的距离为AC=3m，求吊臂的最高点E到地面的高度ED的长．（结果用根号表示．）
解：∵AC⊥CE，∠EAC=60°，AC=3m，
在Rt△ACE中，
∵EC=AC•tan60°=3×
=3m，
∴ED=EC+AB=（3+2）m，
即E点到底面的高度是（3+2）m．
分析：本题的关键是求出EC的长度，在Rt△AEC中，已知了AC=3m，已知了∠EAC=60°，那么可用正切函数求出EC的长，有了EC的长，那么ED=EC+AB就能求出ED的长了．
点评：本题考查了解直角三角形的应用，解直角三角形的过程中，要根据已知条件灵活的选用相应的三角形函数进行求解．
在Rt△ACE中，
∵EC=AC•tan60°=3×
=3m，∴ED=EC+AB=（3
+2）m，即E点到底面的高度是（3
+2）m．分析：本题的关键是求出EC的长度，在Rt△AEC中，已知了AC=3m，已知了∠EAC=60°，那么可用正切函数求出EC的长，有了EC的长，那么ED=EC+AB就能求出ED的长了．
点评：本题考查了解直角三角形的应用，解直角三角形的过程中，要根据已知条件灵活的选用相应的三角形函数进行求解．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
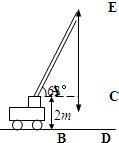17、如图所示，一辆吊车的吊臂以63°的倾角倾斜于水平面，如果这辆吊车支点A距地面的高度AB为2m，且点A到铅垂线ED的距离为AC=15m，则吊臂的最高点E到地面的高度ED的长约为
如图所示，一辆吊车的吊臂以63°的倾角倾斜于水平面，如果这辆吊车支点A距地面的高度AB为2m，且点A到铅垂线ED的距离为AC=15m，求吊臂的最高点E到地面的高度ED的长．（sin63°≈0.89，cos63°≈0.45，tan63°≈1.96，精确到0.1m）