题目内容
【题目】如图,在![]() 中,已知
中,已知![]() ,动点
,动点![]() 同时从
同时从![]() 两点出 发,分别沿
两点出 发,分别沿![]() 方向匀速移动,动点
方向匀速移动,动点![]() 的速度是
的速度是![]() ,动点
,动点![]() 的速度是
的速度是![]() ,当点
,当点![]() 到达点
到达点![]() 时,
时,![]() 两点停止运动,连接
两点停止运动,连接![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() ,试解答下面的问题:
,试解答下面的问题:
![]() 当
当![]() 时,求
时,求![]() 的面积?
的面积?
![]() 当
当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
![]() 是否存在某一时刻
是否存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的角平分线上,若存在,请求出
的角平分线上,若存在,请求出![]() 的值;若不存 在,请说明理由?
的值;若不存 在,请说明理由?
![]() 请用含有
请用含有![]() 的代数式表示四边形
的代数式表示四边形![]() 的面积.
的面积.

【答案】(1)![]() ;(2)t=4;(3)不存在,理由见详解;(4)
;(2)t=4;(3)不存在,理由见详解;(4)![]() .
.
【解析】
(1)根据题意可知当t=1时,AP=2cm,据此过P作PM垂直于BC,进行分析求出![]() 的面积即可;
的面积即可;
(2)由题意可知B在PQ的垂直平分线上即BP=BQ, 设t=m,,则有BP=12-2m, BQ=m,进而进行分析求解即可;
(3)根据题意可知Q在![]() 的平分线上,设CQ为n,AQ为2n,分别求出CQ和BQ,以及当
的平分线上,设CQ为n,AQ为2n,分别求出CQ和BQ,以及当![]() 时,Q在
时,Q在![]() 的平分线上, 比较AP和BP的大小即可;
的平分线上, 比较AP和BP的大小即可;
(4)根据题意连接AQ,并过P作PD垂直于BC,利用![]() 进行分析即可.
进行分析即可.
解:(1)∵在![]() 中,已知
中,已知![]() ,
,
∴AB=12cm,BC= ![]() cm,
cm,
当t=1时,AP=2cm,
∴![]() ,
,![]() ,
,
过P作PM垂直于BC,
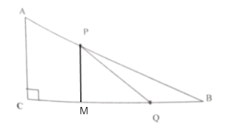
则有![]()
![]() ,
,
∴![]()
![]() .
.
(2)B在PQ的垂直平分线上即BP=BQ,
设t=m,如下图,
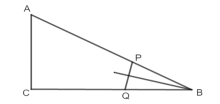
则有BP=12-2m, BQ=m,得出12-2m=m,解得m=4,
∴t=4时,点![]() 在线段
在线段![]() 的垂直平分线上.
的垂直平分线上.
(3)Q在![]() 的平分线上,如图,
的平分线上,如图,
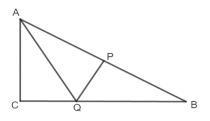
∵![]()
![]()
∴![]() ,
,
∴![]() ,
,
设CQ为n,AQ为2n,则有![]() ,解得n=
,解得n=![]() 或-
或-![]() (舍去),
(舍去),
∴![]()
∴当![]() 时,Q在
时,Q在![]() 的平分线上,此时
的平分线上,此时![]() ,
,
∵![]()
∴不存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的角平分线上.
的角平分线上.
(4)连接AQ,如下图,
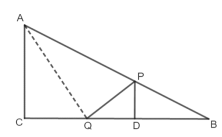
![]() ,
,
过P作PD垂直于BC,如上图,
则有![]() ,
,![]()
∴![]()
![]() .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目





