Question

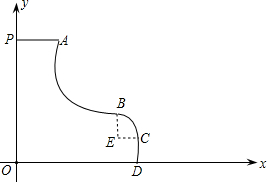
如图是一种新型的滑梯的示意图，其中线段PA是高度为6米的平台，滑道AB是函数y=

10

x

的图象的一部分，滑道BCD是二次函数图象的一部分，两滑道的连接点B为抛物线的顶点，且B点到地面的距离为2米，当甲同学滑到C点时，距地面的距离为1米，距点B的水平距离CE也为1米．
（1）试求滑道BCD所在抛物线的解析式．
（2）试求甲同学从点A滑到地面上D点时，所经过的水平距离．

Answer 1

分析：（1）B点既在双曲线上，又在抛物线上，根据题中数据可求出B点坐标．又因为点B为抛物线的顶点，且B点到地面的距离为2米，当甲同学滑到C点时，距地面的距离为1米，距点B的水平距离CE也为1米．据此可求出解析式．
（2）依据前面的解析式求出A、D的横坐标，之间的差距即为所经过的水平距离．

解答：解：（1）依题意，B点到地面的距离为2米，
设B点坐标为（x，2），
代入y=

10

x

得x=5，
C点距地面的距离为1米，距点B的水平距离CE也为1米，
由题意得：B（5，2），故设滑道BCD所在抛物线的解析式为y=a（x-5）²+2，
将C的坐标（6，1）代入，得a+2=1，解得：a=-1，
则y=-（x-5）²+2，
（2）令y=0，解得x=

2

+5，
又将y=6代入y=

10

x

，
得x=

5

3

；
甲同学从点A滑到地面上D点时，
所经过的水平距离为

2

+5-

5

3

=

10

3

+

2

．

点评：本题考查点的坐标的求法及二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．