题目内容
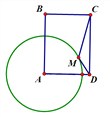
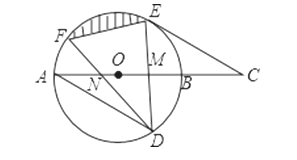
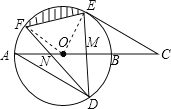
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OB,垂足为M,DE=4,连接AD,过E作AD平行线交AB延长线于点C.
(1)求⊙O的半径;
(2)求证:CE是⊙O的切线;
(3)若弦DF与直径AB交于点N,当∠DNB=30°时,求图中阴影部分的面积.
【答案】(1) ![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】试题分析:(1)连接OE,利用垂径定理,特殊三角形OEM求半径.(2) 由(1)知:∠BOE=60°, 所以易得∠CEO是90°.(3)利用S扇形EOF-S△EOF求面积
试题解析:
解答(1)解:连接OE.
∵DE垂直平分半径OB,
∴OM=![]() OB
OB
∵OB=OE,
∴OM=![]() OE,ME=
OE,ME=![]() DE=2,
DE=2,
∴∠OEM=30°,
∴OE=![]() =
=![]() ;
;
(2)证明:由(1)知:∠BOE=60°,弧BE,
∴∠A=![]() ∠BOE=30°,
∠BOE=30°,
∴∠ADE=60°
∵AD∥CE,
∴∠CED=∠ADE=60°,
∴∠CEO=∠CED+∠OEM=60°+30°=90°,
∴OE⊥EC,
∴EC是⊙O的切线;
(3)解:连接OF.
∵∠DNB=30°,
∵∠DMA=90°,
∴∠MDN=60°,
∴∠EOF=2∠EDF=120°,
∴S阴影=S扇形EOF-S△EOF=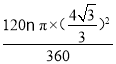 -
-![]() =
=![]() .
.

练习册系列答案
相关题目