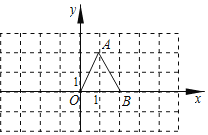题目内容
【题目】如图,直线y=![]() x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.
【答案】(1)y=﹣![]() x+3;(2)①P(﹣
x+3;(2)①P(﹣![]() ,0);②M(
,0);②M(![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).
【解析】
(1)先根据坐标轴上点的特点求出A,B的坐标,进而求出点C坐标,最后用待定系数法即可得出结论;
(2)①设出点M的坐标,利用勾股定理求出BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,最后用勾股定理建立方程求解,即可得出结论;
②设出点M的坐标,进而得出点P,Q坐标,即:得出PQ,最后用面积公式即可得出结论.
解:(1)对于y=![]() x+3,令x=0,y=3,
x+3,令x=0,y=3,
∴B(0,3),
令y=0,
∴![]() x+3=0,
x+3=0,
∴x=﹣6,
∴A(﹣6,0),
∵点C与点A关于y轴对称,
∴C(6,0),
设直线BC的解析式为y=kx+b,
∴![]() ,
,
∴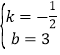 ,
,
∴直线BC的解析式为y=﹣![]() x+3;
x+3;
(2)①设点M(m,0),
∴P(m,![]() m+3),
m+3),
∵B(0,3),C(6,0),
∴BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,
∵∠MBC=90°,
∴△BMC是直角三角形,
∴BM2+BC2=MC2,
∴m2+9+45=(6﹣m)2,
∴m=﹣![]() ,∴P(﹣
,∴P(﹣![]() ,0);
,0);
②设点M(n,0),
∵点P在直线AB:y=![]() x+3上,
x+3上,
∴P(n,![]() n+3),
n+3),
∵点Q在直线BC:y=﹣![]() x+3上,
x+3上,
∴Q(n,﹣![]() n+3),
n+3),
∴PQ=|![]() n+3﹣(﹣
n+3﹣(﹣![]() n+3)|=|n|,
n+3)|=|n|,
∵△PQB的面积为![]() ,
,
∴S△PQB=![]() |n||n|=
|n||n|=![]() n2=
n2=![]() ,
,
∴n=±![]() ,
,
∴M(![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).

【题目】某超市销售每台进价分别为180元、150元的甲、乙两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
甲种型号 | 乙种型号 | ||
第一周 | 2台 | 3台 | 1100元 |
第二周 | 4台 | 5台 | 2000元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求甲、乙两种型号的电器的销售单价;
(2)若超市准备用不多于5000元的金额再采购这两种型号的电器共30台,求甲种型号的电器最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电器能否实现利润超过1900元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【题目】有这样一个问题:探究函数![]() 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)在函数![]() 中,自变量x的取值范围是________.
中,自变量x的取值范围是________.
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | m | … |
①求m的值;
②在平面直角坐标系xOy中,描出以上表中各组对应值为坐标的点,并根据描出的点,画出该函数的图象.

(2)结合函数图象写出该函数的一条性质:________.