Question

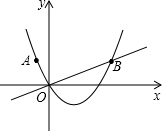（2012•奉贤区二模）已知：直角坐标平面内有点A（-1，2），过原点O的直线l⊥OA，且与过点A、O的抛物线相交于第一象限的B点，若OB=2OA．
（1）求抛物线的解析式；
（2）作BC⊥x轴于点C，设有直线x=m（m＞0）交直线l于P，交抛物线于点Q，若B、C、P、Q组成的四边形是平行四边形，求m的值．

Answer 1

分析：（1）过点A作AH⊥x轴于点H，过点B作BC⊥x轴于点C，根据点A的坐标可得出AH及OH的长度，再由△AHO∽△OCB及OB=2OA可求出点B的坐标，利用待定系数法可求出函数解析式．
（2）先求出直线l的解析式，然后根据B、C、P、Q组成的四边形是平行四边形，结合题意可得PQ=BC，建立方程求解即可得出m的值．

解答：解：（1）过点A作AH⊥x轴于点H，过点B作BC⊥x轴于点C，
由点A坐标为（-1，2）可得AH=2，OH=1，
由直线OB⊥OA，可得△AHO∽△OCB，
故有：

AH

OC

=

OH

BC

=

OA

OB

，
∵OB=2OA，
∴OC=4，BC=2，
∴B（4，2），
设经过点A、O、B的抛物线解析式为y=ax²+bx+c（a≠0），
则

a-b+c=2 16a+4b+c=2 c=0

，
解得

a= 1 2 b=- 3 2 c=0

，
故抛物线解析式为：y=

1

2

x2-

3

2

x．

（2）设直线l的解析式为y=kx（k≠0），
∵直线l经过点B（4，2），
∴直线l的解析式为y=

1

2

x，
∵直线x=m（m＞0）交直线l于P，交抛物线于点Q，
∴设P点坐标为(m，

1

2

m)，点Q坐标为(m，

1

2

m2-

3

2

m)，
∵由B、C、P、Q四点组成的四边形是平行四边形，
∴PQ∥BC且PQ=BC，
即：|

1

2

m-(

1

2

m2-

3

2

m)|=2，
解得m=2±2

2

或m=2，
∵m＞0，
∴m=2

2

+2或2．

点评：此题考查了二次函数的综合题，涉及了相似三角形的判定与性质、平行四边形的判定及解方程的知识，解答此类大综合题关键是能够将所学的知识融会贯通．