题目内容
将平行四边形ABCD对角线的交点与直角坐标系的原点重合,且点A与点B的坐标分别是(-2,-1),(
,-1),则点C和点D的坐标分别为( )
| 1 |
| 2 |
A、(2,1)和(-
| ||
B、(2,-1)和(-
| ||
C、(-2,1)和(
| ||
D、(-1,-2)和(-1,
|
分析:由四边形ABCD对角线的交点与直角坐标系的原点重合,即可得出A、C与B、D分别关于原点对称,进而可求解.
解答:解:∵A、C与B、D分别关于原点对称,点A与点B的坐标分别是(-2,-1),(
,-1),
∴可得C点的坐标为(2,1);点D的坐标为(-
,1).
故此题选A.
| 1 |
| 2 |
∴可得C点的坐标为(2,1);点D的坐标为(-
| 1 |
| 2 |
故此题选A.
点评:此题主要考查坐标与图形的结合问题,即对称问题,熟练掌握平行四边形的性质及对称的而性质,能够求解一些简单的问题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
已知M是平行四边形ABCD的边CD的中点,N为AB边上一点,且AN=3NB,连AM、MN分别交BD于E、F(如图①).
(1)在图②中画出满足上述条件的图形,试用刻度尺在图①、②中量得DE、EF、FB的长度,并填入下表.
由上表可猜想DE、EF、FB间的大小关系是DE=EF=FB.
(2)上述(1)中的猜想DE、EF、FB间的关系成立吗?为什么?
(3)若将平行四边形ABCD改成梯形(其中AB∥CD),且AB=2CD,其它条件不变,此时(1)中猜想DE、EF、FB的关系是否成立?若成立,说明理由;若不成立,求出DE:EF:FB的值.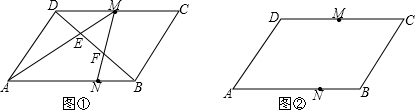
(1)在图②中画出满足上述条件的图形,试用刻度尺在图①、②中量得DE、EF、FB的长度,并填入下表.
| DE的长度 | EF的长度 | FB的长度 | |
| 图①中 | |||
| 图②中 |
(2)上述(1)中的猜想DE、EF、FB间的关系成立吗?为什么?
(3)若将平行四边形ABCD改成梯形(其中AB∥CD),且AB=2CD,其它条件不变,此时(1)中猜想DE、EF、FB的关系是否成立?若成立,说明理由;若不成立,求出DE:EF:FB的值.

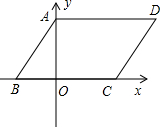 x2-7x+12=0的两个根,且OA>OB.
x2-7x+12=0的两个根,且OA>OB. 24、如图,将平行四边形ABCD的对角线BD向两个方向延长至点E和点F,使BE=DF,求证四边形AECF是平行四边形.
24、如图,将平行四边形ABCD的对角线BD向两个方向延长至点E和点F,使BE=DF,求证四边形AECF是平行四边形. 14、如图,将平行四边形ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,那么对于结论 ①MN∥BC,②MN=AM,下列说法正确的是( )
14、如图,将平行四边形ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,那么对于结论 ①MN∥BC,②MN=AM,下列说法正确的是( ) 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.