题目内容
如图所示是一个直角三角形的苗圃，由一个正方形花坛和两块直角三角形的草皮组成．如果两个直角三角形的两条斜边长分别为3米和6米，则草皮的总面积为（ ）平方米．分析：先根据相似三角形的判定定理得出△AMB∽△CBE，故可得出
=
的值，设CE=x，则BC=2x，在Rt△CBE中根据勾股定理求出x的值，故可得出CE，AB=BC，AM=2AB的值，再根据S草皮=S△CBE+S△AMB=
即可得出结论．
| MB |
| BE |
| AB |
| CE |
| 1 |
| 2 |
解答：解：∵△MDE是直角三角形，四边形ABCD是正方形，
∴∠MAB=∠BCE=90°，∠M+∠ABM=90°，∠ABM+∠CBE=90°，
∴∠M=∠CBE，
∴△AMB∽△CBE，
∴
=
，
∵MB=6，BE=3，
∴
=
=
=2，
∵AB=BC，
∴
=2，
设CE=x，则BC=2x，在Rt△CBE中，
BE2=BC2+CE2，即32=（2x）2+x2，解得x=
，
∴CE=
，AB=BC=
，AM=2AB=
，
∴S草皮=S△CBE+S△AMB=
×
×
+
×
×
=9．
故选B．
∴∠MAB=∠BCE=90°，∠M+∠ABM=90°，∠ABM+∠CBE=90°，
∴∠M=∠CBE，
∴△AMB∽△CBE，
∴
| MB |
| BE |
| AB |
| CE |
∵MB=6，BE=3，
∴
| MB |
| BE |
| AB |
| CE |
| 6 |
| 3 |
∵AB=BC，
∴
| BC |
| CE |
设CE=x，则BC=2x，在Rt△CBE中，
BE2=BC2+CE2，即32=（2x）2+x2，解得x=
3
| ||
| 5 |
∴CE=
3
| ||
| 5 |
6
| ||
| 5 |
12
| ||
| 5 |
∴S草皮=S△CBE+S△AMB=
| 1 |
| 2 |
3
| ||
| 5 |
6
| ||
| 5 |
| 1 |
| 2 |
6
| ||
| 5 |
12
| ||
| 5 |
=9．
故选B．
点评：本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例是解答此题的关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
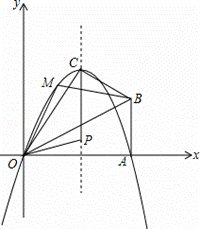
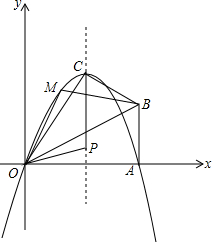（2013•武汉模拟）已知，在Rt△OAB中，∠OAB=90°，∠BOA=30°，AB=2，以O 为原点，OA所在直线为x轴，建立如图所示的平面直角坐标系，点B在第一象限内，将Rt△OAB沿OB折叠后，点A落在第一象限内的点C处．
所示的等腰直角三角形BCD，点E在过A、C、D三点的圆上，且DE⊥BD，连结CE、AD．
