如图.在平面直角坐标系中.直线AB与x轴交于点B.与y轴交于点A.与反比例函数y＝的图象在第二象限交于点C.CE⊥x轴.垂足为点E.tan∠ABO＝.OB＝4,OE＝2．(1)求反比例函数的解析式,(2)若点D是反比例函数图象在第四象限上的点.过点D作DF⊥y轴.垂足为点F.连接OD.BF.如果S△BAF＝4S△DFO.求点D的坐标. 题目和参考答案——青夏教育精英家教网—

题目内容

如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，与反比例函数y＝的图象在第二象限交于点C，CE⊥x轴，垂足为点E，tan∠ABO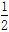＝，OB＝4,OE＝2．

（1）求反比例函数的解析式；

（2）若点D是反比例函数图象在第四象限上的点，过点D作DF⊥y轴，垂足为点F，连接OD、BF，如果S△BAF＝4S△DFO，求点D的坐标.

练习册系列答案

黄冈状元成才路状元大课堂系列答案

相关题目

杨阳同学沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙O，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息汇集如下：

如图，AB∥OH∥CD，相邻两平行线间的距离相等，AC，BD相交于O，OD⊥CD．垂足为D，已知AB=20米，请根据上述信息求标语CD的长度．

下列运算正确的是（）

A．m6÷m2=m3 B．3m2﹣2m2=m2 C．（3m2）3=9m6 D． m•2m2=m2

已知抛物线与x轴交于A、B两点，将这条抛物线的顶点记为C，连接AC、BC，则tan∠CAB的值为（）

A． B． C． D．2

下列计算正确的是（）

A．

B．

C．

D．

在求1＋3＋32＋33＋34＋35＋36＋37＋38的值时，张红发现：从第二个加数起每一个加数都是前一个加数的3倍，于是她假设：S＝1＋3＋32＋33＋34＋35＋36＋37＋38 ①，然后在①式的两边都乘以3，得：3S＝3＋32＋33＋34＋35＋36＋37＋38＋39 ②，

②一①得：3S―S＝39－1，即2S＝39－1，

∴S＝.

得出答案后，爱动脑筋的张红想：如果把“3”换成字母m（m≠0且m≠1），能否求出1＋m＋m2＋m3＋m4＋…＋m2016的值？如能求出，其正确答案是___________.

2016年第一季度，东营市实现生产总值787.68亿元，比上年同期提高了0.9个百分点．787.68亿元用科学记数法表示是_____________元．

为了解学生的体能情况，随机选取了1000名学生进行调查，并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况，整理成以下统计表，其中“√”表示喜欢，“×”表示不喜欢．

（1）估计学生同时喜欢短跑和跳绳的概率；

（2）估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率；

（3）如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大？

如图，在平面直角坐标系中，点P是反比例函数y=（x＞0）图象上的一点，分别过点P作PA⊥x轴于点A，PB⊥y轴于点B．若四边形OAPB的面积为3，则k的值为（）

A．3 B．﹣3 C． D．﹣

试题分类