题目内容
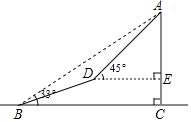
【题目】如图，一座山的一段斜坡BD的长度为600米，且这段斜坡的坡度i=1：3（沿斜坡从B到D时，其升高的高度与水平前进的距离之比）．已知在地面B处测得山顶A的仰角为33°，在斜坡D处测得山顶A的仰角为45°．求山顶A到地面BC的高度AC是多少米？（结果用含非特殊角的三角函数和根式表示即可）
【答案】山顶A到地面BC的高度AC是
米.
【解析】作DH⊥BC于H．设AE=x．在Rt△ABC中，根据tan∠ABC=
，构建方程即可解决问题即可.
作DH⊥BC于H，设AE=x，
∵DH：BH=1：3，
在Rt△BDH中，DH2+（3DH）2=6002，
∴DH=60
，BH=180，
在Rt△ADE中，∵∠ADE=45°，
∴DE=AE=x，
∵又HC=ED，EC=DH，
∴HC=x，EC=60，
在Rt△ABC中，tan33°=
，
∴x=
，
∴AC=AE+EC=+60=
，
答：山顶A到地面BC的高度AC是米.
练习册系列答案
相关题目
【题目】把弹簧的上端固定，在其下端挂物体，下表是测得的弹簧长度
与所挂物体的质量
的一组对应值：
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 15 | 15．5 | 16 | 16．5 | 17 | 17．5 | … |
（1）表中反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）弹簧的原长是_______
，物体每增加
，弹簧的长度增加_________．
（3）请你估测一下当所挂物体为
时，弹簧的长度是______．
