题目内容
如图，圆A，圆B，圆C，圆D，圆E，圆F相互外离（任何两圆之间都不相交，也不包含），它们的半径都是1，顺次连接这六个圆心，得到六边形ABCDEF，则．
（1）六边形ABCDEF的内角和是多少？
（2）图中六个扇形（阴影部分）的面积之和是多少？
解：（1）（6-2）•180=720°；
（2）扇形的面积的和=720×
=2π．
分析：（1）n边形的内角和是（n-2）•180°，代入公式就可以求出六边形ABCDEF的内角和．
（2）扇形的面积公式是：S=
，各个扇形的半径相等，因而六个扇形（阴影部分）的面积之和就等于：六边形的内角和×．
点评：正确记忆多边形的内角和公式，以及扇形的面积公式是解决本题的关键．
（2）扇形的面积的和=720×
=2π．分析：（1）n边形的内角和是（n-2）•180°，代入公式就可以求出六边形ABCDEF的内角和．
（2）扇形的面积公式是：S=
，各个扇形的半径相等，因而六个扇形（阴影部分）的面积之和就等于：六边形的内角和×．点评：正确记忆多边形的内角和公式，以及扇形的面积公式是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，圆A，圆B，圆C，圆D，圆E，圆F相互外离（任何两圆之间都不相交，也不包含），它们的半径都是1，顺次连接这六个圆心，得到六边形ABCDEF，则．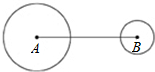
如图，圆A、圆B的半径分别为4、2，且AB=12．若作一圆C使得三圆的圆心在同一直在线，且圆C与圆A外切，圆C与圆B相交于两点，则下列何者可能是圆C的半径长（ ）
