题目内容
平行四边形ABCD的周长32，5AB=3BC，则对角线AC的取值范围为
- A.6＜AC＜10
- B.6＜AC＜16
- C.10＜AC＜16
- D.4＜AC＜16
D
分析：根据平行四边形周长公式求得AB、BC的长度，然后由三角形的三边关系来求对角线AC的取值范围．
解答：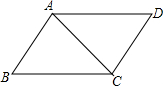
解：∵平行四边形ABCD的周长32，5AB=3BC，
∴2（AB+BC）=2（
BC+BC）=32，
∴BC=10，
∴AB=6，
∴BC-AB＜AC＜BC+AB，即4＜AC＜16．
故选D．
点评：本题考查了平行四边形的性质、三角形三边关系．三角形三边关系：三角形两边之和大于第三边，三角形的两边差小于第三边．
分析：根据平行四边形周长公式求得AB、BC的长度，然后由三角形的三边关系来求对角线AC的取值范围．
解答：
解：∵平行四边形ABCD的周长32，5AB=3BC，∴2（AB+BC）=2（
BC+BC）=32，∴BC=10，
∴AB=6，
∴BC-AB＜AC＜BC+AB，即4＜AC＜16．
故选D．
点评：本题考查了平行四边形的性质、三角形三边关系．三角形三边关系：三角形两边之和大于第三边，三角形的两边差小于第三边．
练习册系列答案
相关题目
（2012•永州）如图，平行四边形ABCD的对角线相交于点O，且AB≠AD，过O作OE⊥BD交BC于点E．若△CDE的周长为10，则平行四边形ABCD的周长为
如图，E、F是平行四边形ABCD的对角线AC上的点，AE=CF．求证：BE=DF．
如图，点E在平行四边形ABCD的对角线BD上．