题目内容
如图所示，直线AB与CD相交于O点，∠1=∠2．若∠AOE=140°，则∠AOC 的度数为
- A.40°
- B.60°
- C.80°
- D.100°
C
分析：由于∠AOE+∠BOE=180°，∠AOE=140°，易求∠2=40°，而∠1=∠2，那么∠BOD=80°，再利用对顶角性质可求∠AOC．
解答：∵
∠AOE+∠BOE=180°，∠AOE=140°，
∴∠2=40°，
∵∠1=∠2，
∴∠BOD=2∠2=80°，
∴∠AOC=∠BOD=80°．
故选C．
点评：本题考查了对顶角、邻补角，解题的关键是先求出∠2．
分析：由于∠AOE+∠BOE=180°，∠AOE=140°，易求∠2=40°，而∠1=∠2，那么∠BOD=80°，再利用对顶角性质可求∠AOC．
解答：∵
∠AOE+∠BOE=180°，∠AOE=140°，∴∠2=40°，
∵∠1=∠2，
∴∠BOD=2∠2=80°，
∴∠AOC=∠BOD=80°．
故选C．
点评：本题考查了对顶角、邻补角，解题的关键是先求出∠2．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
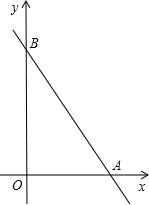如图所示，直线AB与两坐标轴的交点坐标分别是A（6，0），B（0，8），O是坐标系原点．
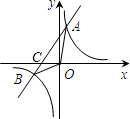如图所示，直线AB与反比例函数
如图所示，直线AB与直线CD相交于点O，EO⊥AB，∠EOD=25°，则∠BOD=
如图所示，直线AB与CD相交于O点，∠1=∠2．若∠AOE=140°，则∠AOC 的度数为（ ）
如图所示，直线AB与CD交于点O，∠BOD=31°36′，OE平分∠BOC，则∠AOD+∠COE=