题目内容
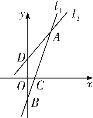
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的解析式为:
的解析式为:![]() ,若将直线
,若将直线![]() 绕
绕![]() 点旋转.如图所示,当直线
点旋转.如图所示,当直线![]() 旋转到
旋转到![]() 位置时,
位置时,![]() 且
且![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ;当直线
;当直线![]() 旋转到
旋转到![]() 位置时,
位置时,![]() 且
且![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)直接写出![]() 、
、![]() 、
、![]() 三点的坐标,连接
三点的坐标,连接![]() ,计算
,计算![]() 的面积;
的面积;
(3)已知坐标平面内一点![]() ,其坐标满足条件
,其坐标满足条件![]() ,当点
,当点![]() 与点
与点![]() 距离最小时,直接写出
距离最小时,直接写出![]() 的值.
的值.
【答案】(1)点A的坐标为![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ;
;![]() ;(3)
;(3)![]()
【解析】
解:(1)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
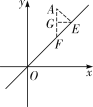
联立解析式,得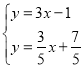 ,
,
解得![]() ,
,
∴点A的坐标为![]() ;
;
(2) ![]() ,
,![]() ,
,![]() ;
;
如解图①,连接DC.
∴![]() ,
,![]() ,
,
∵点![]() ,∴
,∴![]() 底边DB上的高为1,
底边DB上的高为1,
∴![]() .
.
【解法提示】将![]() 代入
代入![]() 得:
得:![]() ,
,
∴![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,解得
,解得![]() ,
,
∴![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
∴![]() ;
;
(3) ![]() .
.
【解法提示】∵![]() ,
,
∴点E在直线![]() 上.
上.
如解图②,过点A作直线![]() 的垂线,垂足为点E,过点A作
的垂线,垂足为点E,过点A作![]() 轴,交直线
轴,交直线![]() 于点F,过点E作
于点F,过点E作![]() ,垂足为点G.
,垂足为点G.
将![]() 代入
代入![]() 得:
得:![]() ,
,
∴![]() .
.
∵点E在直线![]() 上,
上,
∴![]() ,
,
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∵![]() ,
,
∴![]() ,
,
∴点E的纵坐标![]() ,
,
∴![]() .
.

图①
图②
【思维教练】(1)将![]() 和
和![]() 分别代入直线的解析式,得到
分别代入直线的解析式,得到![]() 和
和![]() 的解析式,联立,解关于
的解析式,联立,解关于![]() 、
、![]() 的方程组,可求得点
的方程组,可求得点![]() 的坐标;(2)先求得点
的坐标;(2)先求得点![]() 、
、![]() 、
、![]() 的坐标,然后依据
的坐标,然后依据![]() 求解即可;(3)由点
求解即可;(3)由点![]() 可将问题转化为求点
可将问题转化为求点![]() 到直线
到直线![]() 距离最小时
距离最小时![]() 的值,根据垂线段最短求解.
的值,根据垂线段最短求解.

 口算能手系列答案
口算能手系列答案【题目】某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有![]() 名男生,并对两组男生训练前、后引体向上的个数进行统计分析,得到乙组男生训练前、后引体向上的平均个数分别是
名男生,并对两组男生训练前、后引体向上的个数进行统计分析,得到乙组男生训练前、后引体向上的平均个数分别是![]() 个和
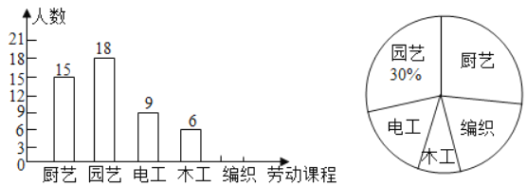
个和![]() 个,及下面不完整的统计表和统计图.
个,及下面不完整的统计表和统计图.
甲组男生训练前、后引体向上个数统计表(单位:个)
甲组 | 男生 | 男生 | 男生 | 男生 | 男生 | 男生 | 平均个数 | 众数 | 中位数 |
训练前 |
|
|
|
|
|
|
|
|
|
训练后 |
|
|
|
|
|
|
|
|
|
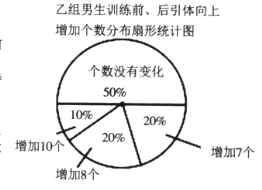
根据以上信息,解答下列问题:
(1)![]() ,
,![]() ,
,![]() ;
;
(2)甲组训练后引体向上的平均个数比训练前增长了 ![]() ;
;
(3)你认为哪组训练效果好?并提供一个支持你观点的理由;
(4)小华说他发现了一个错误:“乙组训练后引体向上个数不变的人数占该组人数的![]() ,所以乙组的平均个数不可能提高
,所以乙组的平均个数不可能提高![]() 个这么多.”你同意他的观点吗?说明理由.
个这么多.”你同意他的观点吗?说明理由.