题目内容
如图,在梯形ABCD中,AD∥BC,∠ABC=90°,∠BCD=45°,点E在BC上,且∠AEB=60°.若AB=2 ,AD=1,求CD和CE的长.(注意:本题中的计算过程和结果均保留根号)
,AD=1,求CD和CE的长.(注意:本题中的计算过程和结果均保留根号)

CD=2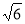 ;CE=2
;CE=2 ﹣1.
﹣1.
【解析】
试题分析:过点D作DF⊥BC,则得四边形ABFD是矩形,由AB=2 ,可得DF=AB=2
,可得DF=AB=2 ,由∠BCD=45°,可得DF=CF,从而可得DF=CF=2
,由∠BCD=45°,可得DF=CF,从而可得DF=CF=2 ,由勾股定理得CD的长,因为AD=1,所以BC=2
,由勾股定理得CD的长,因为AD=1,所以BC=2 +1,根据∠AEB=60°,可得BE的长,从而求出CE的长.
+1,根据∠AEB=60°,可得BE的长,从而求出CE的长.
试题解析:过点D作DF⊥BC,
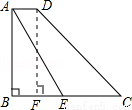
∵AD∥BC,∠ABC=90°,
∴四边形ABFD为矩形,
∵∠BCD=45°,
∴DF=CF,
∵AB=2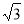 ,
,
∴DF=CF=2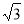 ,
,
∴由勾股定理得CD=2 ;
;
∵AD=1,
∴BF=1,
∴BC=2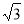 +1,
+1,
∵∠AEB=60°,
∴tan60°=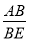 ,
,
∴ ,
,
∴BE=2,
∴CE=BC﹣BE=2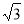 +1﹣2=2
+1﹣2=2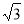 ﹣1.
﹣1.
考点:1、梯形;2、勾股定理;3、三角函数

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目























