题目内容
【题目】已知直线y1=x，y2= 
x+1，y3=﹣ 
x+5的图象如图所示，若无论x取何值，y总取y1 ， y2 ， y3中的最小值，则y的最大值为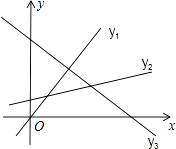 
【答案】
【解析】解：如图，分别求出y1 ， y2 ， y3交点的坐标A（ 
， ）；B（ 
， ）；C（ 
， ）
当x＜ ，y=y1；
当 ≤x＜ ，y=y2；
当 ≤x＜ ，y=y2；
当x≥ ，y=y3 ．
∵y总取y1 ， y2 ， y3中的最小值，
∴y的取值为图中红线所描述的部分，
则y1 ， y2 ， y3中最小值的最大值为C点的纵坐标 ，
∴y最大= ．
【考点精析】本题主要考查了一次函数的图象和性质的相关知识点，需要掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远才能正确解答此题．
练习册系列答案
天天向上一本好卷系列答案
相关题目
