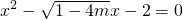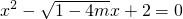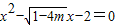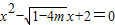题目内容

设方程有一个正根x₁，一个负根x₂，则以|x₁|、|x₂|为根的一元二次方程为（　　）

A．x²-3x-m-2=0

B．x²+3x-m-2=0

C．x2-

1-4m

x-2=0

D．x2-

1-4m

x+2=0

A∵|x₁|+|x₂|=3＞0，但|x₁|•|x₂|=-m-2不能确定它的正负，∴不能选A．
B∵|x₁|+|x₂|=-3＜0，∴不能选B．
C∵|x₁|+|x₂|=

1-4m

＞0，但|x₁|•|x₂|=-2＜0，∴不能选C．
D∵|x₁|+|x₂|=

1-4m

＞0，|x₁|•|x₂|=2＞0，∴选D．
故选D．

练习册系列答案

新概念英语系列答案

新概念课外文言文系列答案

新动力高分攻略系列答案

新导航全程测试卷系列答案

新编初中总复习系列答案

校园英语英语大课堂系列答案

小状元金考卷单元考点梳理系列答案

小学总复习冲刺卷系列答案

小学总复习教程系列答案

通城学典小学总复习系列答案

相关题目

设方程有一个正根x₁，一个负根x₂，则以|x₁|、|x₂|为根的一元二次方程为（　　）

A、x²-3x-m-2=0

B、x²+3x-m-2=0

已知：关于x的一元二次方程mx²-（2m+n）x+m+n=0①．
（1）求证：方程①有两个实数根；
（2）求证：方程①有一个实数根为1；
（3）设方程①的另一个根为x₁，若m+n=2，m为正整数且方程①有两个不相等的整数根时，确定关于x的二次函数y=mx²-（2m+n）x+m+n的解析式；
（4）在（3）的条件下，把Rt△ABC放在坐标系内，其中∠CAB=90°，点A、B的坐标分别为（1，0）、（4，0），BC=5，将△ABC沿x轴向右平移，当点C落在抛物线上时，求△ABC平移的距离．

设方程有一个正根x₁，一个负根x₂，则以|x₁|、|x₂|为根的一元二次方程为

A.
x²-3x-m-2=0
B.
x²+3x-m-2=0
C.
$数学公式$
D.
$数学公式$

设方程有一个正根x₁，一个负根x₂，则以|x₁|、|x₂|为根的一元二次方程为（）
A．x²-3x-m-2=0
B．x²+3x-m-2=0
C．