题目内容
已知反比例函数y1=| m | x |
 与反比例函数的图象相交于另一点B(n,2).
与反比例函数的图象相交于另一点B(n,2).(1)分别求出反比例函数和平移后的一次函数解析式;
(2)求点B的坐标;
(3)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
分析:(1)将A的坐标代入解析式可得m的值,可得反比例函数的解析式;又有A的坐标可得b的值,平移前后k的值不变均为1,可得一次函数的解析式;
(2)将B(n,2)代入解析式可得n的值,进而可得B的值;
(3)观察图象,找反比例函数的图象在一次函数图象上方的部分,可得答案.
(2)将B(n,2)代入解析式可得n的值,进而可得B的值;
(3)观察图象,找反比例函数的图象在一次函数图象上方的部分,可得答案.
解答:解:(1)∵反比例函数y1=
(m≠0)的图象经过点A(-2,1),
∴m=-2.(1分)
∴y1=-
(2分)
设平移后的一次函数解析式为y=x+b,
∵一次函数的图象经过点A,
∴1=-2+b,即b=3.
∴所求一次函数的解析式为y=x+3(3分)
(2)∵一次函数的图象经过B(n,2),(也可由反比例函数解析式求n)
∴n+3=2,即n=-1.
∴B(-1,2)(4分)
(3)根据图象可知,
当x<-2,-1<x<0时,反比例函数的值大于一次函数的值.(5分)
| m |
| x |
∴m=-2.(1分)
∴y1=-
| 2 |
| x |
设平移后的一次函数解析式为y=x+b,
∵一次函数的图象经过点A,
∴1=-2+b,即b=3.
∴所求一次函数的解析式为y=x+3(3分)
(2)∵一次函数的图象经过B(n,2),(也可由反比例函数解析式求n)
∴n+3=2,即n=-1.
∴B(-1,2)(4分)
(3)根据图象可知,
当x<-2,-1<x<0时,反比例函数的值大于一次函数的值.(5分)
点评:此题综合考查了反比例函数,正比例函数等多个知识点,此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
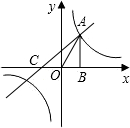 为1.过点A作AB⊥x轴于点B,△AOB的面积1.
为1.过点A作AB⊥x轴于点B,△AOB的面积1.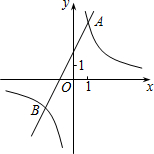 已知反比例函数y1=
已知反比例函数y1= 如图,已知反比例函数
如图,已知反比例函数 已知反比例函数
已知反比例函数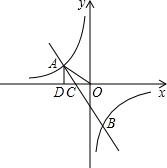 的横坐标为
的横坐标为