题目内容
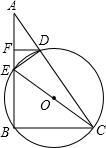 如图,过⊙O外一点A向⊙O引割线AEB,ADC,DF∥BC,交AB于F.若CE过圆心O,D是AC中点.
如图,过⊙O外一点A向⊙O引割线AEB,ADC,DF∥BC,交AB于F.若CE过圆心O,D是AC中点.(1)求证:DF是⊙O的切线;
(2)若FE,FB的长是方程x2-mx+b2=0(b>0)的两个根,且△DEF与△CBE相似.
①试用m的代数式表示b;
②代数式3bm-8
| 3 |
分析:(1)要证DF是⊙O的切线,只需证明FD⊥OD即可.
(2)根据相似三角形的性质及根与系数的关系,即可得到所求的代数式;
(3)将b=
m代入代数式3bm-8
b+7可得:
m2-12m+7,当它有最小值时,m=-
=
.因为△CEB与△CBD全等,可推出EC=2EB,利用勾股定理可得CB的式子,再分别将m的值代入即可求得CB的值.
(2)根据相似三角形的性质及根与系数的关系,即可得到所求的代数式;
(3)将b=
| ||
| 4 |
| 3 |
3
| ||
| 4 |
| -12 | ||||
2•
|
8
| ||
| 3 |
解答:(1)证明:∵CE过圆心O,
∴CB⊥AB;
∵FD∥BC,
∴FD⊥AB;
∵CE过圆心O,D是AC的中点,
∴OD∥AB;
∴FD⊥OD;
∴DF是圆O的切线.
(2)解:∵△DEF∽△CBE,
∴
=
;
∵
=
,BE=BF-EF,
∴
=
,
∴BF=3EF;
∵FE+FB=m,FE•FB=b2,
∴EF=
,BF=
;
∴
•
=b2;
∴b=
m(b>0).
(3)解:将b=
m代入代数式3bm-8
b+7得:
m2-6m+7,
当它有最小值时,m=
=
;
∵△CEB≌△CBD,
∴CB=CD;
∵CD=
AC,
∴CB=
AC,
∴∠A=30°,
∴∠ECB=∠A=30°,
∴EC=2EB;
∴CB=
;
∴CB=
BE=
•
m;
∵m=
,
∴BC=2.
∴CB⊥AB;
∵FD∥BC,
∴FD⊥AB;
∵CE过圆心O,D是AC的中点,
∴OD∥AB;
∴FD⊥OD;
∴DF是圆O的切线.
(2)解:∵△DEF∽△CBE,
∴
| EF |
| BE |
| DF |
| CB |
∵
| DF |
| BC |
| 1 |
| 2 |
∴
| EF |
| BF-EF |
| 1 |
| 2 |
∴BF=3EF;
∵FE+FB=m,FE•FB=b2,
∴EF=
| m |
| 4 |
| 3m |
| 4 |
∴
| m |
| 4 |
| 3m |
| 4 |
∴b=
| ||
| 4 |
(3)解:将b=
| ||
| 4 |
| 3 |
3
| ||
| 4 |
当它有最小值时,m=
| -6 | ||||
2•
|
4
| ||
| 3 |
∵△CEB≌△CBD,
∴CB=CD;
∵CD=
| 1 |
| 2 |
∴CB=
| 1 |
| 2 |
∴∠A=30°,
∴∠ECB=∠A=30°,
∴EC=2EB;
∴CB=
| CE2-BE2 |
∴CB=
| 3 |
| 3 |
| 1 |
| 2 |
∵m=
4
| ||
| 3 |
∴BC=2.
点评:此题考查了圆的切线的判定、相似三角形的性质、全等三角形的性质及勾股定理等知识.要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
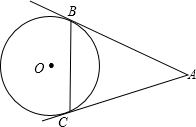 如图,过⊙O外一点A引切线AB、AC,B、C为切点,若∠BAC=60°,BC=8cm,则⊙O的直径是
如图,过⊙O外一点A引切线AB、AC,B、C为切点,若∠BAC=60°,BC=8cm,则⊙O的直径是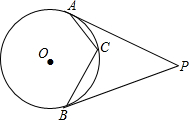 如图,过⊙O外一点P作两条切线,切点分别为A、B,C为劣弧AB上一点,若∠ACB=122°,则∠APB=
如图,过⊙O外一点P作两条切线,切点分别为A、B,C为劣弧AB上一点,若∠ACB=122°,则∠APB=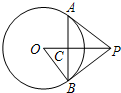 (2012•安庆一模)如图,过⊙O外一点P作⊙O的两条切线PA、PB,切点分别为A、B.下列结论中,正确的是
(2012•安庆一模)如图,过⊙O外一点P作⊙O的两条切线PA、PB,切点分别为A、B.下列结论中,正确的是 如图,过⊙O外一点M作⊙O的两条切线,切点为A、B,连接AB、OA、OB、C、D在⊙O上居于弦AB两端,过点D作⊙O的切线交MA、MB于E、F,连接OE、OF、CA、CB,则图中与∠ACB相等的角(不包含∠ACB)有( )
如图,过⊙O外一点M作⊙O的两条切线,切点为A、B,连接AB、OA、OB、C、D在⊙O上居于弦AB两端,过点D作⊙O的切线交MA、MB于E、F,连接OE、OF、CA、CB,则图中与∠ACB相等的角(不包含∠ACB)有( )