题目内容
37、如图所示，已知EG，FH为正方形ABCD的对角线的交点O，EG⊥FH．求证：四边形EFGH是正方形．
分析：根据正方形的性质求出△COH≌△BOE，得到OE=OH，同理可证OE=OF=OG，根据等量代换得到EG=FH，又因为EG⊥FH，所以四边形EFGH为正方形．
解答：∵四边形ABCD为正方形，
∴OB=OC，∠ABO=∠BCO=45°，∠BOC=90°=∠2+∠3．
∵EG⊥FH，
∴∠1+∠3=90°．
∴∠1=∠2．
∴△COH≌△BOE．
∴OE=OH．
同理可证：OE=OF=OG．
∴OE+OG=OF+OH，即EG=FH．
又∵EG⊥FH，
∴四边形EFGH为正方形．
∴OB=OC，∠ABO=∠BCO=45°，∠BOC=90°=∠2+∠3．
∵EG⊥FH，
∴∠1+∠3=90°．
∴∠1=∠2．
∴△COH≌△BOE．
∴OE=OH．
同理可证：OE=OF=OG．
∴OE+OG=OF+OH，即EG=FH．
又∵EG⊥FH，
∴四边形EFGH为正方形．
点评：根据正方形的性质求证三角形全等是解决本题的关键．
练习册系列答案
相关题目
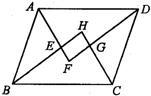53、（体验探究题）如图所示，已知在?ABCD中，各个内角的平分线相交于点E、F、G、H．
如图所示，已知EG，FH为正方形ABCD的对角线的交点O，EG⊥FH．
如图所示，已知EG，FH为正方形ABCD的对角线的交点O，EG⊥FH．