题目内容
如图,AB是![]() 的直径,AF是
的直径,AF是![]() 的切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=
的切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=![]() ,BE=2.
,BE=2.
求证:⑴四边形FADC是菱形;
⑵FC是![]() 的切线.
的切线.
 |
 【证明】⑴连接OC,
【证明】⑴连接OC,
依题意知:AF⊥AB,又CD⊥AB,∴AF∥CD,
又CD∥AD,∴四边形FADC是平行四边形,
由垂径定理得:CE=ED=![]()
 设
设![]() 的半径为R,则OC=R,OE=OB﹣BE=R﹣2,
的半径为R,则OC=R,OE=OB﹣BE=R﹣2,
在![]() ECO中,由勾股定理得:
ECO中,由勾股定理得:![]() ,解得:R=4,
,解得:R=4,
∴AD=![]() ,∴AD=CD,
,∴AD=CD,
因此平行四边形FADC是菱形;
⑵ 连接OF,由⑴得:FC=FA,又OC=OA,FO=FO,
∴![]() FCO≌
FCO≌![]() FAO,∴∠F
FAO,∴∠F![]() CO=∠FAO=
CO=∠FAO=![]() ,
,
因此FC是![]() 的切线.
的切线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
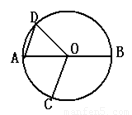
如图,AB是 的直径,点C是半圆的中点,动点P在弦BC上,则
的直径,点C是半圆的中点,动点P在弦BC上,则 可能为( )
可能为( )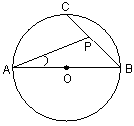
| A.90° | B.50° | C.46° | D.26° |
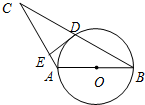 13、如图,AB是的⊙O直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是
13、如图,AB是的⊙O直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是
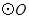 的直径,点C、D在
的直径,点C、D在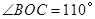 ,
,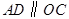 ,则
,则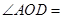 ( )
( )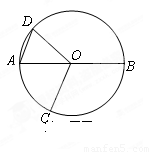
 的直径,点C、D在
的直径,点C、D在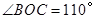 ,
,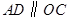 ,则
,则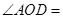
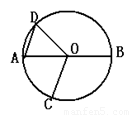
 的直径,点C、D在
的直径,点C、D在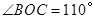 ,
, ,则
,则