Question

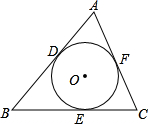如图，⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F，若AB=6，AC=5，BC=7，则AD=

2

，CE=

3

．

Answer 1

分析：首先设AD=x，由⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F，根据切线长定理，可得AF=AD=x，BD=BE=6-x，CE=CF=5-x，继而可得方程：6-x+5-x=7，继而可求得答案．

解答：解：设AD=x，
∵⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F，
∴AF=AD=x，
∵AB=6，AC=5，BC=7，
∴BD=BE=AB-AD=6-x，CE=CF=AC-AF=5-x，
∴6-x+5-x=7，
解得：x=2，
∴AD=2，CE=3．
故答案为：2，3．

点评：此题考查了三角形的内切圆的性质．此题难度适中，注意掌握方程思想与数形结合思想的应用．