题目内容
若直角三角形的两条直角边长分别为3cm、4cm,则斜边上的高为
- A.
 cm
cm - B.
 cm
cm - C.5cm
- D.
 cm
cm
B
分析:先根据勾股定理求出斜边的长度,再根据三角形的面积列式进行计算即可求解.
解答:根据勾股定理,斜边= =5,
=5,
设斜边上的高为h,
则S△= ×3×4=
×3×4= ×5•h,
×5•h,
整理得5h=12,
解得h= cm.
cm.
故选B.
点评:本题考查了勾股定理以及三角形的面积的利用,根据三角形的面积列式求出斜边上的高是常用的方法之一,需熟练掌握.
分析:先根据勾股定理求出斜边的长度,再根据三角形的面积列式进行计算即可求解.
解答:根据勾股定理,斜边=
 =5,
=5,设斜边上的高为h,
则S△=
 ×3×4=
×3×4= ×5•h,
×5•h,整理得5h=12,
解得h=
 cm.
cm.故选B.
点评:本题考查了勾股定理以及三角形的面积的利用,根据三角形的面积列式求出斜边上的高是常用的方法之一,需熟练掌握.

练习册系列答案
相关题目
下列说法正确的是( )
A.若  ,且 ,且 的两条直角边分别是水平和竖直状态,那么 的两条直角边分别是水平和竖直状态,那么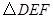 的两条直角边也一定分别是水平和竖直状态 的两条直角边也一定分别是水平和竖直状态 |
B.如果 , , ,那么 ,那么 |
| C.有一条公共边,而且公共边在每个三角形中都是腰的两个等腰三角形一定全等 |
| D.有一条相等的边,而且相等的边在每个三角形中都是底边的两个等腰三角形全等 |

 ,且
,且 的两条直角边分别是水平和竖直状态,那么
的两条直角边分别是水平和竖直状态,那么 的两条直角边也一定分别是水平和竖直状态
的两条直角边也一定分别是水平和竖直状态 ,
, ,那么
,那么