题目内容
 在等腰梯形ABCD中,AB∥DC,AD=BC=6cm,DC=7cm,AB=12cm,点P从点A出发,以每秒3cm的速度沿AD→DC向终点C运动,同时点Q从点B出发,以每秒2cm的速度沿BA向终点A运动.在运动期间,当四边形AQPD为平行四边形时,运动时间为
在等腰梯形ABCD中,AB∥DC,AD=BC=6cm,DC=7cm,AB=12cm,点P从点A出发,以每秒3cm的速度沿AD→DC向终点C运动,同时点Q从点B出发,以每秒2cm的速度沿BA向终点A运动.在运动期间,当四边形AQPD为平行四边形时,运动时间为
- A.3.6秒
- B.4秒
- C.4.4秒
- D.4.8秒
A
分析:设当四边形AQPD为平行四边形时,运动时间为t秒,根据题意可得DP=3t-6,AQ=AB-BQ=12-2t则可得方程3t-6=12-2t,解此方程即可求得答案.
解答: 解:设当四边形AQPD为平行四边形时,运动时间为t秒,
解:设当四边形AQPD为平行四边形时,运动时间为t秒,
∵AD=BC=6cm,DC=7cm,AB=12cm,
∴DP=3t-6(cm),BQ=2tcm,
∴AQ=AB-BQ=12-2t(cm),
∵四边形AQPD为平行四边形,
∴DP=AQ,
即3t-6=12-2t,
解得:t=3.6,
∴运动时间为3.6秒.
故选A.
点评:此题考查了等腰梯形的性质与平行四边形的性质.此题难度适中,注意掌握方程思想与数形结合思想的应用.
分析:设当四边形AQPD为平行四边形时,运动时间为t秒,根据题意可得DP=3t-6,AQ=AB-BQ=12-2t则可得方程3t-6=12-2t,解此方程即可求得答案.
解答:
 解:设当四边形AQPD为平行四边形时,运动时间为t秒,
解:设当四边形AQPD为平行四边形时,运动时间为t秒,∵AD=BC=6cm,DC=7cm,AB=12cm,
∴DP=3t-6(cm),BQ=2tcm,
∴AQ=AB-BQ=12-2t(cm),
∵四边形AQPD为平行四边形,
∴DP=AQ,
即3t-6=12-2t,
解得:t=3.6,
∴运动时间为3.6秒.
故选A.
点评:此题考查了等腰梯形的性质与平行四边形的性质.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.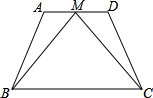 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.