题目内容
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C(-1,0),如图所示:抛物线y=2ax2+ax-32经过点B.
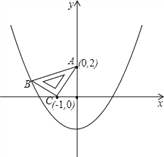
(1)写出点B的坐标;
(2)求抛物线的解析式;
(3)若三角板ABC从点C开始以每秒1个单位长度的速度向x轴正方向平移,求点A落在抛物线上时所用的时间,并求三角板在平移过程扫过的面积;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.
【答案】(1)B(-3,1)(2)y=![]() x2+
x2+![]() x-
x-![]() (3)8.5(4)(1,-1)
(3)8.5(4)(1,-1)
【解析】试题分析:(1)由于△ABC是等腰Rt△,若过B作BD⊥x轴于D,易证得△BCD≌△CAO,则BD=OA=2,BD=OC=1,即可求出B点坐标为:B(-3,1).
(2)将B点坐标代入抛物线的解析式中,即可求出待定系数a的值,也就求得了抛物线的解析式.
(3)设平移后的三角形为△A′B′C′,由于是沿x轴正方向平移,所以A、A′的纵坐标不变,且A′在抛物线的图象上,由此可求出A′的坐标,即可求出AA′,CC′的距离,进而可求出平移过程所用的时间;
那么扫过部分的面积=△ABC的面积+?AA′C′C的面积.
(4)此题要分两种情况进行讨论:
①以C为直角顶点,AC为直角边;可求出直线BC的解析式,联立抛物线的解析式即可求出P点坐标,然后判断CP是否与AC相等即可.
②以A为直角顶点,AC为直角边,方法同①.
试题解析:(1)过B作BD⊥x轴于D;
∵∠BCA=90°,
∴∠BCD=∠CAO=90°-∠ACO;
又∵BC=AC,∠BDC=∠AOC=90°,
∴△BDC≌△COA;
∴AO=DC=2,BD=OC=1,
∴B(-3,1).
(2)由于抛物线过B点,则有:2a×9+(-3)a-32=1,
解得a=![]()
∴y=![]() x2+
x2+![]() x-
x-![]() .
.
(3)设平移后的三角形为△A′B′C′;
当y=2时,![]() x2+
x2+![]() x-
x-![]() =2
=2
解得x=3(负值舍去);
∴A′(3,2),C′(2,0);
∴平移过程所用去的时间为3÷1=3秒;
S扫=S△ABC+S四边形AA′C′C=![]() ×(
×(![]() )2+3×2=8.5(平方单位).
)2+3×2=8.5(平方单位).
(4)①若以AC为直角边,C为直角顶点;
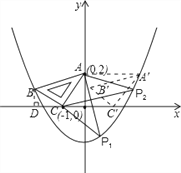
设直线BC交抛物线y=![]() x2+
x2+![]() x-
x-![]() 于P1,
于P1,
易求得直线BC的解析式为y=-![]() x-
x-![]() ;不难求得P1(1,-1),此时CP1=AC;
;不难求得P1(1,-1),此时CP1=AC;
∴△ACP1为等腰直角三角形;
②若以AC为直角边,点A为直角顶点;
过A作AF∥BC,交抛物线y=![]() x2+
x2+![]() x-
x-![]() 于P2,易求得直线AF的解析式为y=-
于P2,易求得直线AF的解析式为y=-![]() x+2;
x+2;
因为以AC为直角边,点A为直角顶点的等腰Rt△ACP的顶点P有两种情况,即AC=AP2,AC⊥AP2,
∵CO=1,AO=2,
只有P到y轴距离为2,到x轴距离为1,且在第一象限符合题意,
此时P2(2,1),
或者P点在第三象限P3(-2,3)符合题意,
经检验点P2(2,1)与P3(-2,3)不在抛物线上,
所以,符合条件的点P有1个:(1,-1).