题目内容
 如图所示,四边形ABCD中,BD平分∠ABC,点E在BC边上,AB=BE,AD=DC,求证:∠A与∠C互补.
如图所示,四边形ABCD中,BD平分∠ABC,点E在BC边上,AB=BE,AD=DC,求证:∠A与∠C互补.
证明:∵BD平分∠ABC,
∴∠ABD=∠EBD.
又∵AB=EB,BD=BD,
∴△ABD≌△EBD.
∴∠A=∠BED,AD=ED.
又∵AD=DC.
∴DE=DC,
∴∠C=∠DEC.
∵∠BED+∠DEC=180°,
∴∠A+∠C=180°,
即∠A与∠C互补.
分析:利用BD是角平分线,易得∠ABD=∠EBD,而AB=EB,BD=BD,利用SAS可证△ABD≌△EBD,于是∠A=∠BED,AD=ED,而AD=DC,那么DC=DE,就有∠DEC=∠C,由于∠BED+∠DEC=180°,等量代换,就有∠A+∠C=180°,即∠A、∠C互补.
点评:本题考查了角平分线的性质、全等三角形的判定和性质、等量代换等知识.等量代换是做题时常常用到的方法.
∴∠ABD=∠EBD.
又∵AB=EB,BD=BD,
∴△ABD≌△EBD.
∴∠A=∠BED,AD=ED.
又∵AD=DC.
∴DE=DC,
∴∠C=∠DEC.
∵∠BED+∠DEC=180°,
∴∠A+∠C=180°,
即∠A与∠C互补.
分析:利用BD是角平分线,易得∠ABD=∠EBD,而AB=EB,BD=BD,利用SAS可证△ABD≌△EBD,于是∠A=∠BED,AD=ED,而AD=DC,那么DC=DE,就有∠DEC=∠C,由于∠BED+∠DEC=180°,等量代换,就有∠A+∠C=180°,即∠A、∠C互补.
点评:本题考查了角平分线的性质、全等三角形的判定和性质、等量代换等知识.等量代换是做题时常常用到的方法.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G.
21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G. 12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )
12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )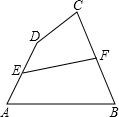 如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
