Question

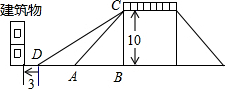（2013•黄埔区一模）为方便市民低碳生活绿色出行，市政府计划改造如图所示的人行天桥：天桥的高是10米，原坡面倾斜角∠CAB=45°．
（1）若新坡面倾斜角∠CDB=28°，则新坡面的长CD长是多少？（精确到0.1米）
（2）若新坡角顶点D前留3米的人行道，要使离原坡角顶点A处10米的建筑物不拆除，新坡面的倾斜角∠CDB度数的最小值是多少？（精确到1°）

Answer 1

分析：（1）在Rt△BCD中，已知BC=10，∠CDB=28°，解直角三角形即可求出CD的长度；
（2）根据∠CAB=45°，可得AB=10，已知建筑物距A为10米，可得BD最大值为17米，在Rt△BCD中，解直角三角形求出∠CDB的度数即可．

解答：（1）在Rt△BCD中，
∵BC=10，∠CDB=28°，
∴CD=

BC

sin∠CDB

=

10

sin28°

≈21.3（米），
答：新坡面的长为21.3米
（2）∵∠CAB=45°，
∴AB=CB=10，
又建筑物离原坡角顶点A处10米，即建筑物离天桥底点B的距离为20米，
当DB取最大值时，∠CDB达最小值，
要使建筑物不被拆掉DB的最大值为20-3=17，
则tan∠CDB=

CB

DB

=

10

17

≈0.588，
∴∠CDB≈31°．
答：若新坡角顶点D前留3米的人行道，要使离原坡角顶点A处10米的建筑物不拆除，新坡面的倾斜角的最小值是31°．

点评：本题考查了解直角三角形的应用，难度适中，解答本题的关键是构造直角三角形并解直角三角形．