Question

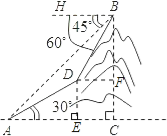
【题目】如图所示，某校九年级(3)班的一个学习小组进行测量小山高度的实践活动．部分同学在山脚A点处测得山腰上一点D的仰角为30°，并测得AD的长度为180米．另一部分同学在山顶B点处测得山脚A点的俯角为45°，山腰D点的俯角为60°，请你帮助他们计算出小山的高度BC．(计算过程和结果都不取近似值)

Answer 1

【答案】米

【解析】

试题首先根据题意分析图形；过点D作DE⊥AC于点E，作DF⊥BC于点F；构造本题涉及到的两个直角三角形，根据图形分别求解可得DE与BF的值，再利用BC=DE+BF，进而可求出答案．

解：如图，过点D作DE⊥AC于点E，作DF⊥BC于点F，

则有DE∥FC，DF∥EC．

∵∠DEC=90°，

∴四边形DECF是矩形，

∴DE=FC．

∵∠HBA=∠BAC=45°，

∴∠BAD=∠BAC﹣∠DAE=45°﹣30°=15度．

又∵∠ABD=∠HBD﹣∠HBA=60°﹣45°=15°，

∴△ADB是等腰三角形．∴AD=BD=180（米）．

在Rt△AED中，sin∠DAE=sin30°=，

∴DE=180sin30°=180×=90（米），∴FC=90米．

在Rt△BDF中，∠BDF=∠HBD=60°，sin∠BDF=sin60°=，

∴BF=180sin60°=180×（米）．

∴BC=BF+FC=90+90=90（+1）（米）．

答：小山的高度BC为90（+1）米．