Question

【题目】已知线段AB=42，点C是线段AB的中点，点D是线段CB的中点，点E在线段AB上，且CE= AC，求线段DE的长．

Answer 1

【答案】解：∵线段AB=42，点C为AB中点，
∴AC=BC= AB= ×42=21，
∵点D为BC中点，
∴CD=BD= BC= ×21=10.5，
∵CE= AC，
∴CE= ×21=7，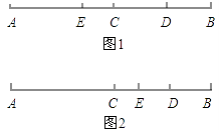

如图1，DE=CD+CE=10.5+7=17.5；
如图2，DE=CD﹣CE=10.5﹣7=3.5．
综上所述，线段DE的长是17.5或3.5．
【解析】根据点C是线段AB的中点，点D是线段CB的中点，可求AC、BC，CD、BD，再由已知条件CE= AC,可求CE，根据DE=CD+CE或DE=CD﹣CE
线段DE的长可求。