题目内容
 已知:如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.
已知:如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.
求:(1)求∠CDB的度数;
(2)当AD=2时,求对角线BD的长和梯形ABCD的面积.
解:(1)∵在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,
∴∠CBA=∠A=60°.
∵BD平分∠ABC,
∴∠CDB=∠ABD= ∠CBA=30°,
∠CBA=30°,
(2)

在△ABD中,∵∠ADB=180°-∠A-∠ABD=90°.
∴BD=AD•tanA=2tan60°=2 .
.
过点D作DH⊥AB,垂足为H,
∴DH=AD•sinA=2sin60°= .
.
∵∠CDB=∠CBD= ∠CBD=30°,∴DC=BC=AD=2.
∠CBD=30°,∴DC=BC=AD=2.
∵AB=2AD=4,
∴S梯形ABCD= (AB+CD)DH=
(AB+CD)DH= ×(4+2)×
×(4+2)× =3
=3 .
.
分析:(1)由平行线及角平分线的性质可得∠CDB=∠ABD= ∠ABC,根据等腰梯形两底角相等的性质可得∠CDB的具体度数;
∠ABC,根据等腰梯形两底角相等的性质可得∠CDB的具体度数;
(2)利用30°的正切值可得BD的长度,也就求得了AB的长度,利用60°正弦值可得梯形的高,进而利用梯形的面积公式可得梯形的面积.
点评:综合考查了解直角三角形的知识及梯形的性质;利用或构造特殊的直角三角形是解决本题的关键.
∴∠CBA=∠A=60°.
∵BD平分∠ABC,
∴∠CDB=∠ABD=
 ∠CBA=30°,
∠CBA=30°,(2)

在△ABD中,∵∠ADB=180°-∠A-∠ABD=90°.
∴BD=AD•tanA=2tan60°=2
 .
.过点D作DH⊥AB,垂足为H,
∴DH=AD•sinA=2sin60°=
 .
.∵∠CDB=∠CBD=
 ∠CBD=30°,∴DC=BC=AD=2.
∠CBD=30°,∴DC=BC=AD=2.∵AB=2AD=4,
∴S梯形ABCD=
 (AB+CD)DH=
(AB+CD)DH= ×(4+2)×
×(4+2)× =3
=3 .
.分析:(1)由平行线及角平分线的性质可得∠CDB=∠ABD=
 ∠ABC,根据等腰梯形两底角相等的性质可得∠CDB的具体度数;
∠ABC,根据等腰梯形两底角相等的性质可得∠CDB的具体度数;(2)利用30°的正切值可得BD的长度,也就求得了AB的长度,利用60°正弦值可得梯形的高,进而利用梯形的面积公式可得梯形的面积.
点评:综合考查了解直角三角形的知识及梯形的性质;利用或构造特殊的直角三角形是解决本题的关键.

练习册系列答案
相关题目
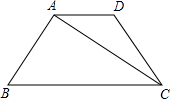 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.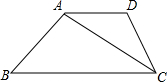 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,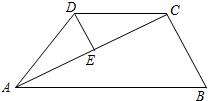 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=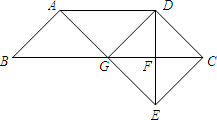 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.