题目内容
如图，是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形，如果正方形的面积是13，小正方形的面积是1，直角三角形的两条边是分别是a，b，则a+b和的平方的值（ ）| A、13 | B、19 | C、25 | D、169 |
分析：由图可知直角三角形的两直角边a-b=1，且a2+b2=13，解方程可求得a、b，计算（a+b）2即可．
解答：解：由图可知，直角三角形两直角边a、b符合a-b=1，
且正方形面积为13，则边长为
，
∴a2+b2=13，
解得a=3，b=2，
∴（a+b）2=25．
故选 C．
且正方形面积为13，则边长为
| 13 |
∴a2+b2=13，
解得a=3，b=2，
∴（a+b）2=25．
故选 C．
点评：本题考查了勾股定理在直角三角形中的灵活运用，本题中根据a、b的关系，解a、b的值是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，是由四个全等的大等腰直角三角形和四个全等的小等腰直角三角形拼成，图形旋转α角度后能与自身重合，则α可能是（ ）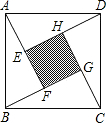
如图，是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形．已知直角三角形的两个直角边长分别是1，2，小明随机地在大正方形及其内部区域投针，则针扎在小正方形区域的概率是
