题目内容
【题目】如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,正方形
,正方形![]() 的点
的点![]() 在线段
在线段![]() 上,点
上,点![]() ,
,![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在点
在点![]() 的右侧,
的右侧,![]() .将正方形
.将正方形![]() 沿
沿![]() 轴正方向平移,得到正方形
轴正方向平移,得到正方形![]() ,当点
,当点![]() 与点
与点![]() 重合时停止运动.设平移的距离为
重合时停止运动.设平移的距离为![]() ,正方形
,正方形![]() 与
与![]() 重合部分的面积为
重合部分的面积为![]() .
.
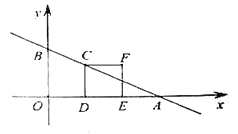
(1)求直线![]() 的解析式;
的解析式;
(2)求点![]() 的坐标;
的坐标;
(3)求![]() 与
与![]() 的解析式,并直接写出自变量
的解析式,并直接写出自变量![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3) 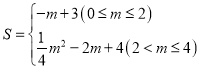 .
.
【解析】
(1)将A,E的坐标代入解析式即可解答
(2)根据题意可知CD=2,将其代入解析式,即可求出点C
(3)根据题意可分情况讨论:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,即可解答
,即可解答
(1)设直线![]() 的解析式为
的解析式为![]() ,因为经过点
,因为经过点![]() ,点
,点![]() .
.
![]() ,解得:
,解得: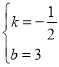 ,∴
,∴![]() .
.
(2)当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() .
.
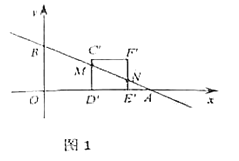
(3)当![]() 时,如图1.
时,如图1.
点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
∴当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() ,
,
∴![]() .
.
∴![]() .
.
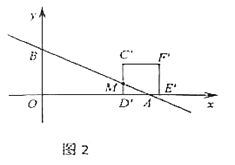
当![]() 时,如图2.
时,如图2.
![]()
∴![]()
综上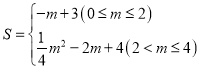 .
.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目




