题目内容
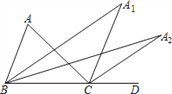
【题目】如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1,则∠A1= ______ ;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…;∠An-1BC与∠An-1CD的平分线相交于点An,要使∠An的度数为整数,则n的值最大为 ______ .
【答案】 32 6
【解析】由三角形的外角性质得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∵∠ABC的平分线与∠ACD的平分线交于点A1,
∴∠A1BC=![]() ∠ABC,∠A1CD=
∠ABC,∠A1CD=![]() ∠ACD,
∠ACD,
∴∠A1+∠A1BC=![]() (∠A+∠ABC)=
(∠A+∠ABC)= ![]() ∠A+∠A1BC,
∠A+∠A1BC,
∴∠A1=![]() ∠A=
∠A=![]() ×64°=32°;
×64°=32°;
∵A1B、A1C分别平分∠ABC和∠ACD,
∴∠ACD=2∠A1CD,∠ABC=2∠A1BC,
而∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,
∴∠A=2∠A1,
∴∠A1=![]() ∠A,
∠A,
同理可得∠A1=2∠A2,
∴∠A2=![]() ∠A,
∠A,
∴∠A=2n∠An,
∴∠An=(![]() )n∠A=
)n∠A=![]() ,
,
∵∠An的度数为整数,
∵n=6.
故答案为:32°,6.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
