题目内容
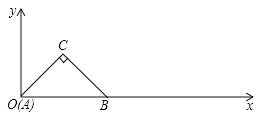
【题目】如图,海中一渔船在A处与小岛C相距70海里,若该渔船由西向东航行30海里到达B处,此时测得小岛C位于B的北偏东30°方向上,则该渔船此时与小岛C之间的距离是_____海里.
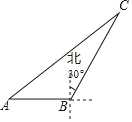
【答案】50
【解析】分析:过点C作CD⊥AB于点D,由题意得∠BCD=30°,设BC=x,解直角三角形即可得到BD、CD,进而得出AD,根据“AD2+CD2=AC2”列方程求解可得.
详解:过点C作CD⊥AB于点D,
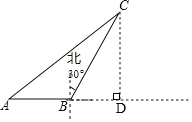
由题意得∠BCD=30°,
设BC=x,
在Rt△BCD中,
BD=BCsin30°=![]() x,CD=BCcos30°=
x,CD=BCcos30°=![]() x;
x;
∴AD=30+![]() x,
x,
∵AD2+CD2=AC2,
∴(30+![]() x)2+(
x)2+(![]() x)2=702,
x)2=702,
解得:x=50(负值舍去),
即渔船此时与C岛之间的距离为50海里.
故答案为:50.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
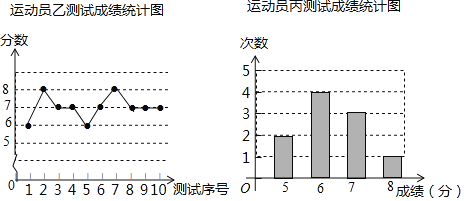
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)