ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋžŨĄĒŌŌÁ―ļöđĪģĖķÓđēÍŽģÐĩĢŌŧÏîÖþ·ČÎÎņĢŽžŨķÓĩĨķĀĘĐđĪÍęģÉīËÏîČÎÎņąČŌŌķÓĩĨķĀĘĐđĪÍęģÉīËÏîČÎÎņķāÓÃ![]() ĖėĢŽĮŌžŨķÓĩĨķĀĘĐđĪ
ĖėĢŽĮŌžŨķÓĩĨķĀĘĐđĪ![]() ĖėšÍŌŌķÓĩĨķĀĘĐđĪ
ĖėšÍŌŌķÓĩĨķĀĘĐđĪ![]() ĖėĩÄđĪŨũÁŋÏāÍŽĢŪ
ĖėĩÄđĪŨũÁŋÏāÍŽĢŪ
![]() žŨĄĒŌŌÁ―ķÓĩĨķĀÍęģÉīËÏîČÎÎņļũÐčķāÉŲĖėĢŋ
žŨĄĒŌŌÁ―ķÓĩĨķĀÍęģÉīËÏîČÎÎņļũÐčķāÉŲĖėĢŋ
![]() ÉčÏČÓÉžŨķÓĘĐđĪ
ÉčÏČÓÉžŨķÓĘĐđĪ![]() ĖėĢŽÔŲÓÉŌŌķÓĘĐđĪ
ĖėĢŽÔŲÓÉŌŌķÓĘĐđĪ![]() ĖėĢŽļÕšÃÍęģÉÖþ·ČÎÎņĢŽĮó
ĖėĢŽļÕšÃÍęģÉÖþ·ČÎÎņĢŽĮó![]() Óë
Óë![]() ÖŪžäĩÄšŊĘýđØÏĩĘ―ĢŪ
ÖŪžäĩÄšŊĘýđØÏĩĘ―ĢŪ
![]() ÔÚ
ÔÚ![]() ĩÄĖõžþÏÂĢŽČôÃŋĖėÐčļķļøžŨķÓĩÄÖþ··ŅÓÃΊ
ĩÄĖõžþÏÂĢŽČôÃŋĖėÐčļķļøžŨķÓĩÄÖþ··ŅÓÃΊ![]() ÍōÔŠĢŽÐčļķļøŌŌķÓĩÄÖþ··ŅÓÃΊ
ÍōÔŠĢŽÐčļķļøŌŌķÓĩÄÖþ··ŅÓÃΊ![]() ÍōÔŠĢŽĮŌžŨĄĒŌŌÁ―ķÓĘĐđĪĩÄŨÜĖėĘýēŧģŽđý
ÍōÔŠĢŽĮŌžŨĄĒŌŌÁ―ķÓĘĐđĪĩÄŨÜĖėĘýēŧģŽđý![]() ĖėĢŽÔōČįšÎ°ēÅÅžŨĄĒŌŌÁ―ķÓĘĐđĪĩÄĖėĘýĢŽĘđĘĐđĪ·ŅÓÃŨîÉŲĢŽēĒĮóģöŨîÉŲ·ŅÓÃĢŪ
ĖėĢŽÔōČįšÎ°ēÅÅžŨĄĒŌŌÁ―ķÓĘĐđĪĩÄĖėĘýĢŽĘđĘĐđĪ·ŅÓÃŨîÉŲĢŽēĒĮóģöŨîÉŲ·ŅÓÃĢŪ
Ąūīð°ļĄŋ![]() žŨķÓ
žŨķÓ![]() ĖėĢŽŌŌķÓ
ĖėĢŽŌŌķÓ![]() ĖėĢŧ
ĖėĢŧ![]() Ģŧ
Ģŧ![]() ĩąžŨĄĒŌŌÁ―ķÓķžŨö
ĩąžŨĄĒŌŌÁ―ķÓķžŨö![]() ĖėĘąĢŽŨîÉŲ
ĖėĘąĢŽŨîÉŲ![]() ÍōÔŠĢŪ
ÍōÔŠĢŪ
Ąū―âÎöĄŋ
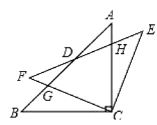
ĢĻ1ĢĐÉčžŨķÓĩĨķĀÍęģÉīËÏîČÎÎņÐčŌŠ![]() ĖėĢŽÔōŌŌķÓĩĨķĀÍęģÉīËÏîČÎÎņÐčŌŠ
ĖėĢŽÔōŌŌķÓĩĨķĀÍęģÉīËÏîČÎÎņÐčŌŠ![]() ĖėĢŽļųūÝžŨķÓĩĨķĀĘĐđĪ45ĖėšÍŌŌķÓĩĨķĀĘĐđĪ30ĖėĩÄđĪŨũÁŋÏāÍŽ―ĻÁĒ·―ģĖĮóģöÆä―âžīŋÉĢŧ
ĖėĢŽļųūÝžŨķÓĩĨķĀĘĐđĪ45ĖėšÍŌŌķÓĩĨķĀĘĐđĪ30ĖėĩÄđĪŨũÁŋÏāÍŽ―ĻÁĒ·―ģĖĮóģöÆä―âžīŋÉĢŧ
![]() ÓÉžŨŌŌÍęģÉĩÄđĪŨũÁŋÖŪšÍΊ
ÓÉžŨŌŌÍęģÉĩÄđĪŨũÁŋÖŪšÍΊ![]() ĢŽÁКŊĘýđØÏĩĘ―ĢŽąäÐÎŋÉĩÃīð°ļĢŽ
ĢŽÁКŊĘýđØÏĩĘ―ĢŽąäÐÎŋÉĩÃīð°ļĢŽ
![]() ÉčžŨķÓ°ēÅÅ
ÉčžŨķÓ°ēÅÅ![]() ĖėĢŽĀûÓÃŨÜĖėĘýēŧģŽđý
ĖėĢŽĀûÓÃŨÜĖėĘýēŧģŽđý![]() ĖėĢŽÁÐēŧĩČĘ―Įó―â
ĖėĢŽÁÐēŧĩČĘ―Įó―â![]() ĩÄ·ķΧĢŽÔŲÁÐģöŨÜ·ŅÓÃĩÄĩÄđØÏĩĘ―ĢŽĀûÓÃŌŧīΚŊĘýĩÄÐÔÖĘŋÉĩÃīð°ļĢŪ
ĩÄ·ķΧĢŽÔŲÁÐģöŨÜ·ŅÓÃĩÄĩÄđØÏĩĘ―ĢŽĀûÓÃŌŧīΚŊĘýĩÄÐÔÖĘŋÉĩÃīð°ļĢŪ
―âĢš![]() ÉčžŨķÓĩĨķĀÍęģÉÐčŌŠ
ÉčžŨķÓĩĨķĀÍęģÉÐčŌŠ![]() ĖėĢŽÔōŌŌķÓĩĨķĀÍęģÉÐčŌŠ
ĖėĢŽÔōŌŌķÓĩĨķĀÍęģÉÐčŌŠ![]() ĖėĢŽÓÉĖâŌâĩÃĢš
ĖėĢŽÓÉĖâŌâĩÃĢš
![]() ĢŽ
ĢŽ
![]()
![]()
ūžėŅéĢš![]() ĘĮÔ·―ģĖĩÄļųĢŽÔō
ĘĮÔ·―ģĖĩÄļųĢŽÔō![]()
![]() žŨķÓĩĨķĀÍęģÉÐčŌŠ
žŨķÓĩĨķĀÍęģÉÐčŌŠ![]() ĖėĢŽÔōŌŌķÓĩĨķĀÍęģÉÐčŌŠ
ĖėĢŽÔōŌŌķÓĩĨķĀÍęģÉÐčŌŠ![]() ĖėĢŪ
ĖėĢŪ
![]() ÓÉĖâŌâĩÃĢš
ÓÉĖâŌâĩÃĢš![]()
![]()
![]() ÉčžŨķÓ°ēÅÅ
ÉčžŨķÓ°ēÅÅ![]() ĖėĢŽÔōŌŌķÓ°ēÅÅ
ĖėĢŽÔōŌŌķÓ°ēÅÅ![]() ĖėĢŽ
ĖėĢŽ
![]()
―âĩÃĢš![]()
ÓÖŨÜ·ŅÓÃ![]()
![]()
![]() ĘąĢŽžīžŨŌŌķž°ēÅÅ
ĘąĢŽžīžŨŌŌķž°ēÅÅ![]() ĖėĢŽŨÜ·ŅÓÃŨîÉŲĢŽ
ĖėĢŽŨÜ·ŅÓÃŨîÉŲĢŽ
īËĘąĢŽŨÜ·ŅÓÃ![]() ÍōÔŠĢŪ
ÍōÔŠĢŪ

ĄūĖâÄŋĄŋÄģÍÁēúđŦËūŨéÖŊ20ÁūÆûģĩŨ°ÔËžŨĄĒŌŌĄĒąûČýÖÖÍÁĖØēúđē120ķÖČĨÍâĩØÏúĘÛ°īžÆŧŪ20ÁūģĩķžŌŠŨ°ÔË,ÃŋÁūÆûģĩÖŧÄÜŨ°ÔËÍŽŌŧÖÖÍÁĖØēú,ĮŌąØÐëŨ°Âú,ļųūÝÏÂąíĖáđĐĩÄÐÅÏĒ,―âīðŌÔÏÂÎĘĖâ
ÍÁĖØēúÖÖĀā | žŨ | ŌŌ | ąû |
ÃŋÁūÆûģĩÔËÔØÁŋ(ķÖ) | 8 | 6 | 5 |
ÃŋķÖÍÁĖØēúŧņĀû(°ŲÔŠ) | 12 | 16 | 10 |
(1)ÉčŨ°ÔËžŨÖÖÍÁĖØēúĩÄģĩÁūĘýΊx,Ũ°ÔËŌŌÖÖÍÁĖØēúĩÄģĩÁūĘýΊy,ĮóyÓëxÖŪžäĩÄšŊĘýđØÏĩĘ―Ģŧ
(2)ČįđûŨ°ÔËÃŋÖÖÍÁĖØēúĩÄģĩÁūķžēŧÉŲÓÚ3Áū,ÄĮÃīģĩÁūĩÄ°ēÅÅ·―°ļÓОļÖÖ?ēĒÐīģöÃŋÖÖ°ēÅÅ·―°ļĢŧ
(3)ČôŌŠĘđīËīÎÏúĘÛŧņĀûŨîīó,ÓĶēÉÓÃ(2)ÖÐÄÄÖÖ°ēÅÅ·―°ļ?ēĒĮóģöŨîīóĀûČóĩÄÖĩ