题目内容
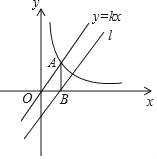
【题目】如图，正比例函数y＝kx与反比例函数y＝
（x＞0）的图象有个交点A，AB⊥x轴于点B．平移正比例函数y＝kx的图象，使其经过点B（2，0），得到直线l，直线l与y轴交于点C（0，﹣3）
（1）求k和m的值；
（2）点M是直线OA上一点过点M作MN∥AB，交反比例函数y＝（x＞0）的图象于点N，若线段MN＝3，求点M的坐标．
【答案】（1）
，m=6 （2）（
，
）或（
， 
）
【解析】
（1）利用待定系数法即可解决问题；(2)设点M（x，
x）,N(x，
)，利用MN//AB， MN=3，列方程求解即可.
（1）∵直线l与y轴交于点(0，-3)，且过点 B(2，0)，
设直线l的解析式为y=ax-3，代入点B(2，0)，解得a=，
∵直线l与正比例函数y=kx平行，∴k=a=，
∵y=x过点 A，AB⊥x轴于点B，∴A(2，3)
∵y=
过点A，∴m=6；
（2）设点M（x，x）,N(x，)，
∵MN//AB， MN=3， ∴ x-=3，或x-=-3，
解得：
，或
(舍去负值)，
∴点M的坐标为（，）或（， 
）
【题目】自2016年国庆后，许多高校均投放了使用手机就可随用的共享单车．某运营商为提高其经营的A品牌共享单车的市场占有率，准备对收费作如下调整：一天中，同一个人第一次使用的车费按0.5元收取，每增加一次，当次车费就比上次车费减少0.1元，第6次开始，当次用车免费．具体收费标准如下：
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时，就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿，得到如下数据：
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
（Ⅰ）写出
的值；
（Ⅱ）已知该校有5000名师生，且A品牌共享单车投放该校一天的费用为5800元．试估计：收费调整后，此运营商在该校投放A品牌共享单车能否获利? 说明理由．
