题目内容
（2012•乐陵市二模）如图，在平面直角坐标系中，线段AB的端点坐标为A（-1，2），B（3，1），若直线y=kx-2与线段AB有交点，则k的值可能是（ ）分析：先求出直线y=kx-2与y轴的交点C的坐标，再利用待定系数法求出直线AC、BC的解析式，然后根据直线与线段AB有交点，则k值小于AC的k值，或大于BC的k值，然后根据此范围进行选择即可．
解答：
解：令x=0，则y=0•k-2=-2，
所以直线y=kx-2与y轴的交点坐标为（0，-2），
设直线AC的解析式为y=mx+n，
则
，
解得
．
所以直线AC的解析式为y=-4x-2，
设直线BC的解析式为y=ex+f，
则
，
解得
．
所以直线BC的解析式为y=x-2，
若直线y=kx-2与线段AB有交点，则k的取值范围是k≤-4或k≥1，
纵观各选项，只有D选项符号．
故选D．
解：令x=0，则y=0•k-2=-2，所以直线y=kx-2与y轴的交点坐标为（0，-2），
设直线AC的解析式为y=mx+n，
则
|
解得
|
所以直线AC的解析式为y=-4x-2，
设直线BC的解析式为y=ex+f，
则
|
解得
|
所以直线BC的解析式为y=x-2，
若直线y=kx-2与线段AB有交点，则k的取值范围是k≤-4或k≥1，
纵观各选项，只有D选项符号．
故选D．
点评：本题考查了两直线相交的问题，根据已知直线求出与y轴的交点坐标，然后求出两直线的解析式是解题的关键．
练习册系列答案
相关题目
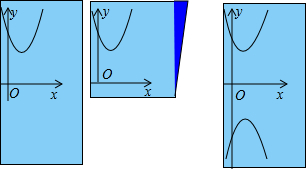（2012•乐陵市二模）如图，在一张纸上作出函数y=x2-2x+3的图象，沿x轴把这张纸对折，描出与抛物线y=x2-2x+3关于x轴对称的抛物线，则描出的这条抛物线的解析式为
（2012•乐陵市二模）如图，把等腰直角△ABC放在直角坐标系内，其中∠CAB=90°，点A、B的坐标分别为（1，0）（4，0），将等腰直角△ABC沿x轴向右平移，当点C落在直线y=x-2上时，则等腰直角△ABC被直线y=x-2扫过的面积为
（2012•乐陵市二模）操作观察：