题目内容
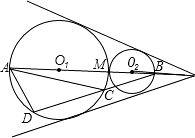 如图,⊙O1和⊙O2外切于M,它们的两条外公切线的夹角为60°,连心线与⊙O1与⊙O2分别交于A、B(异于M点),过B作直线交⊙O1于C、D两点,求:cot∠BAC•cot∠BAD的值.
如图,⊙O1和⊙O2外切于M,它们的两条外公切线的夹角为60°,连心线与⊙O1与⊙O2分别交于A、B(异于M点),过B作直线交⊙O1于C、D两点,求:cot∠BAC•cot∠BAD的值.
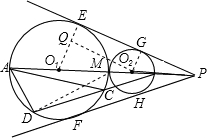 解:如图,
解:如图,由题设可得O1E⊥PE,O1F⊥PF,O1E=O1F,
∴O1在∠EPF的平分线上,同理O2在∠EPF的平分线上,
∴PA为∠EPF的平分线,
∵O2Q∥PE,∴∠QO2O1=∠EPO1=30°,
∴O1Q=
 O1O2,
O1O2,设大、小圆半径为R、r,则O1Q=R-r,O1O2=R+r,
∴R-r=
 (R+r),∴R=3r,
(R+r),∴R=3r,∵∠ACM=∠ADM=90°,
∴cot∠BAC•cot∠BAD=
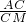 •
• ,
,由△BAC∽△BDM,△BAD∽△BCM可得,
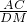 =
= ,
, =
=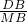 ,
,∴cot∠BAC•cot∠BAD=
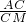 •
• =
= •
•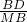 =
=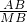 =
= =4.
=4.分析:可过O1、O2作EF边的垂线,可得出PA为∠EPF的平分线,再过O2作PE的平行线,可得O1Q=
 O1O2,进而求出大、小圆半径之间的关系,再由相似三角形对应边成比例,通过线段之间的转化,即可求解.
O1O2,进而求出大、小圆半径之间的关系,再由相似三角形对应边成比例,通过线段之间的转化,即可求解.点评:本题主要考查了圆与圆之间的位置关系以及相似三角形的判定及性质问题,能够掌握并熟练运用.

练习册系列答案
相关题目
 20、已知:如图,⊙O1和⊙O2相交于A、B两点,动点P在⊙O2上,且在⊙1外,直线PA、PB分别交⊙O1于C、D,问:⊙O1的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明.
20、已知:如图,⊙O1和⊙O2相交于A、B两点,动点P在⊙O2上,且在⊙1外,直线PA、PB分别交⊙O1于C、D,问:⊙O1的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明.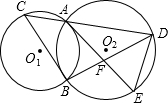 长⊙O1相交于C点,连接BC,过A点作AE∥BC与⊙O相交于E点,与BD相交于F点.
长⊙O1相交于C点,连接BC,过A点作AE∥BC与⊙O相交于E点,与BD相交于F点.
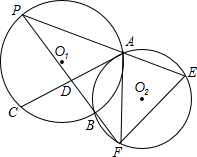 、PB的延长线分别交⊙O2于点E、F,PB交AC于D.
、PB的延长线分别交⊙O2于点E、F,PB交AC于D. 16、如图.⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点,求证:AB⊥AC.
16、如图.⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点,求证:AB⊥AC. (2001•黄冈)已知,如图,⊙O1和⊙O2内切于点P,过点P的直线交⊙O1于点D,交⊙O2于点E;DA与⊙O2相切,切点为C.
(2001•黄冈)已知,如图,⊙O1和⊙O2内切于点P,过点P的直线交⊙O1于点D,交⊙O2于点E;DA与⊙O2相切,切点为C.