Question

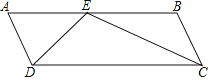
【题目】已知:如图①，将的菱形沿对角线剪开，将沿射线方向平移，得到点为边上一点（点不与点、点重合），将射线绕点逆时针旋转，与的延长线交于点，连接．

①求证:；

②探究的形状；

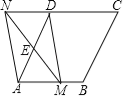
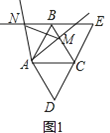
如图②，若菱形变为正方形，将射线绕点逆时针旋转，原题其他条件不变，中的①和②两个结论是否仍然成立？若成立，请直接写出结论；若不成立，请写出变化后的结论并证明．

Answer 1

【答案】（1）①证明见解析；②△是等边三角形，理由见解析；（2）①∠=∠成立，理由见解析；②不成立，△是等腰直角三角形，理由见解析．

【解析】

（1）①先由菱形可知四边相等，再由∠D＝60°得等边△ADC和等边△ABC，则对角线AC与四边都相等，利用ASA证明△ANB≌△AMC，得结论；

②根据有一个角是60°的等腰三角形是等边三角形得出：△AMN是等边三角形；

（2）①成立，根据正方形得45°角和射线AM绕点A逆时针旋转45°，证明△ANB∽△AMC，得∠ANB＝∠AMC；

②不成立，△AMN是等腰直角三角形，利用①中的△ANB∽△AMC，得比例式进行变形后，再证明△NAM∽△BAD，则△AMN是等腰直角三角形．

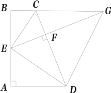
（1）如图1，①∵四边形是菱形，

∴，

∵∠60°，

∴△ADC和△ABC是等边三角形，

∴，∠BAC60°，

∵∠60°，

∴∠=∠，

由△ADC沿射线DC方向平移得到△BCE，可知∠CBE60°，

∵∠ABC60°，

∴∠ABN60°，

∴∠ABN∠ACB60°

∴△≌△，

∴∠=∠；

②如图1，△是等边三角形，理由是：

由△≌△，

∴AMAN，

∵∠60°，

∴△是等边三角形；

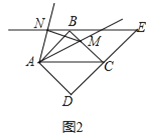
（2）①如图2，∠=∠成立，理由是：

在正方形ABCD中，

∴∠BAC∠DAC=∠BCA45°，

∵∠NAM45°，

∴∠=∠，

由平移得：∠EBC∠CAD45°，

∵∠ABC=90°，

∴∠ABN180°90°45°45°，

∴∠ABN∠ACM45°，

∴△∽△，

∴∠=∠；

②如图2，不成立，

△是等腰直角三角形，理由是：

∵△∽△，

∴，

∴，

∵∠=∠=45°，

∴△∽△，

∴∠=∠=90°，

∴△是等腰直角三角形.